题目内容
14.$\underset{lim}{△x→0}\frac{cos(1+△x)-cos1}{△x}$的值为-sin1.分析 利用导数的定义即可得出.
解答 解:$\underset{lim}{△x→0}\frac{cos(1+△x)-cos1}{△x}$=(cosx)′|x=1=-sin1,
故答案为:-sin1.
点评 本题考查了导数的定义,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.sin(-60°)的值为( )
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | $-\frac{1}{2}$ |
5.若直线$\left\{\begin{array}{l}x=1-2t\\ y=2+3t\end{array}\right.$(t为参数)与直线4x+ky=1垂直,则常数k=( )
| A. | -6 | B. | $-\frac{1}{6}$ | C. | 6 | D. | $\frac{1}{6}$ |
9.一个盒子中有20个大小形状相同的小球,其中5个红球,5个黄球,10个蓝球,从盒子中任取一球,若它不是红球,则它是蓝球的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |
19.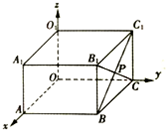 如图,长方体ABCO-A1B1C1O1中,|OA|=4,|OC|=6,|OO1|=2,BC1与B1C相交于点P,则点P的坐标是( )
如图,长方体ABCO-A1B1C1O1中,|OA|=4,|OC|=6,|OO1|=2,BC1与B1C相交于点P,则点P的坐标是( )
 如图,长方体ABCO-A1B1C1O1中,|OA|=4,|OC|=6,|OO1|=2,BC1与B1C相交于点P,则点P的坐标是( )
如图,长方体ABCO-A1B1C1O1中,|OA|=4,|OC|=6,|OO1|=2,BC1与B1C相交于点P,则点P的坐标是( )| A. | (6,2,1) | B. | (1,2,6) | C. | (4,6,2) | D. | (2,6,1) |
3.我市某玩具生产公司根据市场调查分析,决定调整产品生产方案,准备每天生产A,B,C三种玩具共100个,且C玩具至少生产20个.每天生产时间不超过10小时,已知生产这些玩具每个所需工时(分钟)和所获利润如下表:
(1)用每天生产A玩具个数x与B玩具个数y表示每天的利润ω(元)
(2)怎样分配生产任务才能使每天的利润最大,最大利润是多少?
| 玩具名称 | A | B | C |
| 工时(分钟) | 5 | 7 | 4 |
| 利润(元) | 5 | 6 | 3 |
(2)怎样分配生产任务才能使每天的利润最大,最大利润是多少?
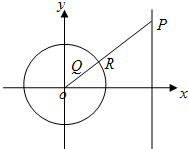 已知圆C:x2+y2=4,直线l:x=8,以原点O为极点,x轴非负半轴为极轴建立极坐标系.
已知圆C:x2+y2=4,直线l:x=8,以原点O为极点,x轴非负半轴为极轴建立极坐标系.