题目内容
11.已知定义在R上的函数y=f(x),其周期为2,且x∈(-1,1)时f(x)=1+x2,函数g(x)=$\left\{\begin{array}{l}{1+sinπx(x≥0)}\\{1-\frac{1}{x}(x<0)}\end{array}\right.$,则函数h(x)=f(x)-g(x)在区间[-3,5]上的零点个数为( )| A. | 11 | B. | 10 | C. | 9 | D. | 8 |
分析 分别研究:f(x)=g(x)在区间[-3,0)有2个交点,在区间(0,5]上,有6个交点,即可得出结论.
解答 解:①x<0时,由题意,f(x)=g(x),
画出函数f(x),g(x)在[-3,0)上的图象,如图示: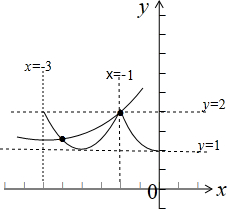
在区间[-3,-2),(-2,0)间分别有一个交点,
故函数f(x),g(x)在[-3,0)上有2个交点,
②x≥0时,在区间[0,5]上,由图象可得有6个交点,零点有6个,
故选:D.
点评 键是把函数有零点的问题,转化成两函数在某区间内有交点的问题,属中档题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
19.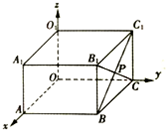 如图,长方体ABCO-A1B1C1O1中,|OA|=4,|OC|=6,|OO1|=2,BC1与B1C相交于点P,则点P的坐标是( )
如图,长方体ABCO-A1B1C1O1中,|OA|=4,|OC|=6,|OO1|=2,BC1与B1C相交于点P,则点P的坐标是( )
 如图,长方体ABCO-A1B1C1O1中,|OA|=4,|OC|=6,|OO1|=2,BC1与B1C相交于点P,则点P的坐标是( )
如图,长方体ABCO-A1B1C1O1中,|OA|=4,|OC|=6,|OO1|=2,BC1与B1C相交于点P,则点P的坐标是( )| A. | (6,2,1) | B. | (1,2,6) | C. | (4,6,2) | D. | (2,6,1) |
16.在等比数列3,6,12,…中,第5项为( )
| A. | 18 | B. | 24 | C. | 36 | D. | 48 |
3.我市某玩具生产公司根据市场调查分析,决定调整产品生产方案,准备每天生产A,B,C三种玩具共100个,且C玩具至少生产20个.每天生产时间不超过10小时,已知生产这些玩具每个所需工时(分钟)和所获利润如下表:
(1)用每天生产A玩具个数x与B玩具个数y表示每天的利润ω(元)
(2)怎样分配生产任务才能使每天的利润最大,最大利润是多少?
| 玩具名称 | A | B | C |
| 工时(分钟) | 5 | 7 | 4 |
| 利润(元) | 5 | 6 | 3 |
(2)怎样分配生产任务才能使每天的利润最大,最大利润是多少?
20.($\sqrt{x}-\frac{1}{x}$)9展开式中的常数项是( )
| A. | -36 | B. | 36 | C. | -84 | D. | 84 |
18.已知等差数列{an}和{bn}的前n项和分别为Sn,Tn,且$\frac{{S}_{n}}{{T}_{n}}$=$\frac{3n+1}{2n}$,则$\frac{a_5}{b_5}$=( )
| A. | $\frac{8}{5}$ | B. | $\frac{9}{14}$ | C. | $\frac{5}{8}$ | D. | $\frac{14}{9}$ |
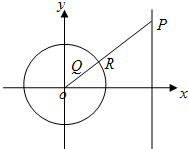 已知圆C:x2+y2=4,直线l:x=8,以原点O为极点,x轴非负半轴为极轴建立极坐标系.
已知圆C:x2+y2=4,直线l:x=8,以原点O为极点,x轴非负半轴为极轴建立极坐标系.