题目内容
8．一个几何体的三视图如图所示，则该几何体的体积为8．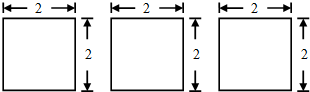
分析 根据几何体的三视图，得出该几何体是棱长为2的正方体，求出它的体积即可．
解答 解：根据几何体的三视图，得；
该几何体是棱长为2的正方体，
所以它的体积为23=8．
故答案为：8．
点评 本题考查了利用空间几何体的三视图求体积的应用问题，是基础题目．
练习册系列答案
相关题目
19．
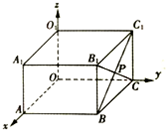如图，长方体ABCO-A1B1C1O1中，|OA|=4，|OC|=6，|OO1|=2，BC1与B1C相交于点P，则点P的坐标是（ ）
如图，长方体ABCO-A1B1C1O1中，|OA|=4，|OC|=6，|OO1|=2，BC1与B1C相交于点P，则点P的坐标是（ ）| A． | （6，2，1） | B． | （1，2，6） | C． | （4，6，2） | D． | （2，6，1） |
16．在等比数列3，6，12，…中，第5项为（ ）
| A． | 18 | B． | 24 | C． | 36 | D． | 48 |
3．我市某玩具生产公司根据市场调查分析，决定调整产品生产方案，准备每天生产A，B，C三种玩具共100个，且C玩具至少生产20个．每天生产时间不超过10小时，已知生产这些玩具每个所需工时（分钟）和所获利润如下表：
（1）用每天生产A玩具个数x与B玩具个数y表示每天的利润ω（元）
（2）怎样分配生产任务才能使每天的利润最大，最大利润是多少？
| 玩具名称 | A | B | C |
| 工时（分钟） | 5 | 7 | 4 |
| 利润（元） | 5 | 6 | 3 |
（2）怎样分配生产任务才能使每天的利润最大，最大利润是多少？
20．（$\sqrt{x}-\frac{1}{x}$）9展开式中的常数项是（ ）
| A． | -36 | B． | 36 | C． | -84 | D． | 84 |
14．已知$M=\left\{{（x，y）\left|{y=\sqrt{1-{x^2}}}\right.}\right\}$，N={（x，y）|y=x+b}，若M∩N≠∅，则实数b的范围是（ ）
| A． | [-1，1] | B． | $[{-\sqrt{2}，1}]$ | C． | $[{-1，\sqrt{2}}]$ | D． | $[{-\sqrt{2}，\sqrt{2}}]$ |
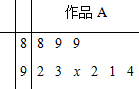我校开展“爱我河南，爱我方城”摄影比赛，9位评委为参赛作品A给出的分数如茎叶图所示，记分员在去掉一个最高分和一个最低分后，计算的平均分为91，复核员在复核时，发现一个数字（茎叶图中的x）无法看清，若记分员计算无误，则数字x应该是1．