题目内容
6．某单位组织4个部门的职工旅游，规定每个部门只能在韶山、衡山、张家界3个景区中任选一个，假设各部门选择每个景区是等可能的．则3个景区都有部门选择的概率是$\frac{4}{9}$．分析 根据题意，首先由分步计数原理计算4个部门选择3个景区可能出现的结果数目，再记“3个景区都有部门选择”为事件A，由分步计数原理计算可得其包含的情况数目，进而由古典概型公式计算可得答案．
解答 解：根据题意，每个部门都有3种情况可选，则4个部门选择3个景区有34=81种不同的选法，
记“3个景区都有部门选择”为事件A，
如果3个景区都有部门选择，则某一个景区必须有2个部门选择，其余2个景区各有1个部门选择，
分2步分析：
①、从4个部门中任选2个作为1组，另外2个部门各作为1组，共3组，共有C42=6种分法，
②、每组选择不同的景区，共有A33=6种选法，
∴3个景区都有部门选择可能出现的结果数为6×6=36种；
则P（A）=$\frac{36}{81}$=$\frac{4}{9}$；
故答案为：$\frac{4}{9}$．
点评 本题考查古典概型的计算以及排列、组合的运用，关键要利用分步计数原理和排列组合公式计算出“3个景区都有部门选择”的选法数目．
练习册系列答案
相关题目
19．
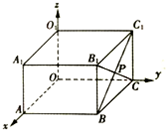如图，长方体ABCO-A1B1C1O1中，|OA|=4，|OC|=6，|OO1|=2，BC1与B1C相交于点P，则点P的坐标是（ ）
如图，长方体ABCO-A1B1C1O1中，|OA|=4，|OC|=6，|OO1|=2，BC1与B1C相交于点P，则点P的坐标是（ ）| A． | （6，2，1） | B． | （1，2，6） | C． | （4，6，2） | D． | （2，6，1） |
20．（$\sqrt{x}-\frac{1}{x}$）9展开式中的常数项是（ ）
| A． | -36 | B． | 36 | C． | -84 | D． | 84 |
14．已知$M=\left\{{（x，y）\left|{y=\sqrt{1-{x^2}}}\right.}\right\}$，N={（x，y）|y=x+b}，若M∩N≠∅，则实数b的范围是（ ）
| A． | [-1，1] | B． | $[{-\sqrt{2}，1}]$ | C． | $[{-1，\sqrt{2}}]$ | D． | $[{-\sqrt{2}，\sqrt{2}}]$ |
18．已知等差数列{an}和{bn}的前n项和分别为Sn，Tn，且$\frac{{S}_{n}}{{T}_{n}}$=$\frac{3n+1}{2n}$，则$\frac{a_5}{b_5}$=（ ）
| A． | $\frac{8}{5}$ | B． | $\frac{9}{14}$ | C． | $\frac{5}{8}$ | D． | $\frac{14}{9}$ |
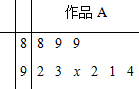我校开展“爱我河南，爱我方城”摄影比赛，9位评委为参赛作品A给出的分数如茎叶图所示，记分员在去掉一个最高分和一个最低分后，计算的平均分为91，复核员在复核时，发现一个数字（茎叶图中的x）无法看清，若记分员计算无误，则数字x应该是1．