题目内容
9．电灯泡使用时间在1000小时以上概率为0.2，则3个灯泡在使用1000小时后坏了1个的概率是（ ）| A． | 0.128 | B． | 0.096 | C． | 0.104 | D． | 0.384 |
分析 由题意知3个相互独立的灯泡使用的时间能否超过1000小时，可以看做一个做了3次独立重复试验的概率，根据独立重复试验的公式得到结果．
解答 解：∵灯泡的耐用时间超过1000小时的概率为0.2，
3个相互独立的灯泡使用的时间能否超过1000小时，
可以看做一个做了3次独立重复试验的概率，
∴3个灯泡在使用1000小时后坏了1个的概率是C31×0.8×0.22=0.096，
故选：B
点评 本题考查n次独立重复试验中恰好发生k次的概率，本题解题的关键是看出本试验符合独立重复试验，本题是一个基础题．
练习册系列答案
相关题目
20．下列关于函数f（x）=-2sin2x-cos4x（x∈R）的说法正确的是（ ）
| A． | f（x）的最小正周期为2π | B． | f（x）的最大值为-1 | ||
| C． | f（x）是偶函数 | D． | f（x）在[$\frac{π}{12}$，$\frac{π}{4}$]上单调增 |
17．“sinA=$\frac{1}{2}$”是“A=30°”的（ ）
| A． | 充分而不必要条件 | B． | 既不充分也不必要条件 | ||
| C． | 充分必要条件 | D． | 必要而不充分条件 |
4．sin（-60°）的值为（ ）
| A． | $\frac{{\sqrt{3}}}{2}$ | B． | $\frac{1}{2}$ | C． | $-\frac{{\sqrt{3}}}{2}$ | D． | $-\frac{1}{2}$ |
19．
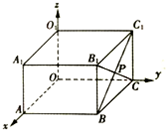如图，长方体ABCO-A1B1C1O1中，|OA|=4，|OC|=6，|OO1|=2，BC1与B1C相交于点P，则点P的坐标是（ ）
如图，长方体ABCO-A1B1C1O1中，|OA|=4，|OC|=6，|OO1|=2，BC1与B1C相交于点P，则点P的坐标是（ ）| A． | （6，2，1） | B． | （1，2，6） | C． | （4，6，2） | D． | （2，6，1） |