题目内容
【题目】已知函数  ,则关于x的方程[f(x)]2﹣f(x)+a=0(a∈R)的实数解的个数不可能是( )
,则关于x的方程[f(x)]2﹣f(x)+a=0(a∈R)的实数解的个数不可能是( )
A.2
B.3
C.4
D.5
【答案】A
【解析】解:当x<0时,f′(x)=﹣ ![]() ﹣1<0,
﹣1<0,
∴f(x)在(﹣∞,0)上是减函数,
当x>0时,f(x)=|lnx|= ![]() ,
,
∴f(x)在(0,1)上是减函数,在[1,+∞)上是增函数,
做出f(x)的大致函数图象如图所示:
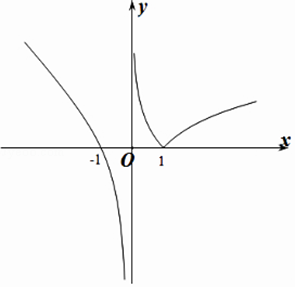
设f(x)=t,则当t<0时,方程f(x)=t有一解,
当t=0时,方程f(x)=t有两解,
当t>0时,方程f(x)=t有三解.
由[f(x)]2﹣f(x)+a=0,得t2﹣t+a=0,
若方程t2﹣t+a=0有两解t1,t2,则t1+t2=1,
∴方程t2﹣t+a=0不可能有两个负实数根,
∴方程[f(x)]2﹣f(x)+a=0不可能有2个解.
故选A.

练习册系列答案
相关题目