Question

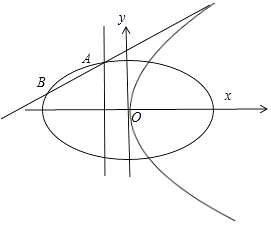
【题目】已知椭圆 的右焦点与抛物线y2=4x的焦点F重合，且椭圆的离心率是 ，如图所示．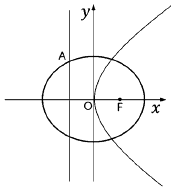

（1）求椭圆的标准方程；
（2）抛物线的准线与椭圆在第二象限相交于点A，过点A作抛物线的切线l，l与椭圆的另一个交点为B，求线段AB的长．

Answer 1

【答案】
（1）解：根据题意，得F（1，0），∴c=1，

又e= ，∴a=2，∴b2=a2﹣c2=3，

故椭圆的标准方程为：

（2）解：抛物线的准线方程为x=﹣1

由 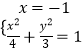，解得 ， ，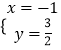

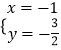由A位于第二象限，则A（﹣1， ），

过点A作抛物线的切线l的方程为：

即直线l：4x﹣3y﹣4=0

由 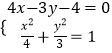整理得

整理得：ky2﹣4y+4k+6=0，

当k=0，解得：y= ，不符合题意，

当k≠0，由直线与抛物线相切，则△=0，

∴（﹣4）2﹣4k（4k+6）=0，解得：k= 或k=﹣2，

当k= 时，直线l的方程y﹣ = （x+1），

则 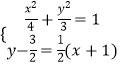，整理得：（x+1）2=0，

直线与椭圆只有一个交点，不符合题意，

当k=﹣2时，直线l的方程为y﹣ =﹣2（x+1），

由 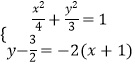，整理得：19x2+8x﹣11=0，解得：x1=﹣1，x2= ，

则y1= ，y2=﹣ ，

由以上可知点A（﹣1， ），B（ ，﹣ ），

∴丨AB丨= = ，

综上可知：线段AB长度为

【解析】（1）根据题意得F（1，0），即c=1，再通过e= 及c2=a2﹣b2计算可得椭圆的方程；（2）将准线方程代入椭圆方程，求得A点坐标，求得抛物线的切线方程，由△=0，求得k的值，分别代入椭圆方程，求得B点坐标，利用两点之间的距离公式，即可求得线段AB的长．