题目内容
【题目】在如图所示的五面体中,面ABCD为直角梯形,∠BAD=∠ADC= ![]() ,平面ADE⊥平面ABCD,EF=2DC=4AB=4,△ADE是边长为2的正三角形.
,平面ADE⊥平面ABCD,EF=2DC=4AB=4,△ADE是边长为2的正三角形. 
(Ⅰ)证明:BE⊥平面ACF;
(Ⅱ)求二面角A﹣BC﹣F的余弦值.
【答案】证明:(Ⅰ)取AD中点O,以O为原点,OA为x轴,
过O作AB的平行线为y轴,OE为z轴,
建立空间直角坐标系,

则B(1,1,0),E(0,0, ![]() ),A(1,0,0),
),A(1,0,0),
C(﹣1,2,0),F(0,4, ![]() ),
),
![]() =(﹣1,﹣1,
=(﹣1,﹣1, ![]() ),
), ![]() =(﹣1,4,
=(﹣1,4, ![]() ),
),
![]() =(﹣2,2,0),
=(﹣2,2,0),
![]() =1﹣4+3=0,
=1﹣4+3=0, ![]() =2﹣2=0,
=2﹣2=0,
∴BE⊥AF,BE⊥AC,
又AF∩AC=A,∴BE⊥平面ACF.
(Ⅱ)解: ![]() =(﹣2,1,0),
=(﹣2,1,0), ![]() =(﹣1,3,
=(﹣1,3, ![]() ),
),
设平面BCF的法向量 ![]() =(x,y,z),
=(x,y,z),
则 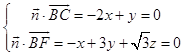 ,取x=1,得
,取x=1,得 ![]() =(1,2,﹣
=(1,2,﹣ ![]() ),
),
平面ABC的法向量 ![]() =(0,0,1),
=(0,0,1),
设二面角A﹣BC﹣F的平面角为θ,
则cosθ= ![]() =
= 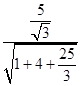 =
= ![]() .
.
∴二面角A﹣BC﹣F的余弦值为 ![]() .
.
【解析】(Ⅰ)取AD中点O,以O为原点,OA为x轴,过O作AB的平行线为y轴,OE为z轴,建立空间直角坐标系,利用向量法能证明BE⊥平面ACF.(Ⅱ)求出平面BCF的法向量和平面ABC的法向量,利用向量法能求出二面角A﹣BC﹣F的余弦值.
【考点精析】解答此题的关键在于理解直线与平面垂直的判定的相关知识,掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目


