题目内容
7.已知F1,F2是椭圆C:$\frac{{x}^{2}}{3}$+$\frac{{y}^{2}}{4}$=1的两个焦点,过F1的直线与椭圆C交于M,N两点,则△F2MN的周长为8.分析 利用椭圆的定义可知|F1M|+|F2M|和|F1N|+|F2N|的值,进而把四段距离相加即可求得答案.
解答 解:利用椭圆的定义可知,|F1M|+|F2M|=2a=4,|F1N|+|F2N|=2a=4,
∴△MNF2的周长为|F1M|+|F2M|+F1N|+|F2N|=4+4=8.
故答案为:8.
点评 本题主要考查了椭圆的简单性质.解题的关键是利用椭圆的定义.

练习册系列答案
相关题目
8.已知x>0,y>0,且2x+y=1,则$\frac{1}{x}+\frac{1}{y}$的最小值是( )
| A. | 6 | B. | 4$\sqrt{2}$ | C. | 3+2$\sqrt{2}$ | D. | 3+4$\sqrt{2}$ |
19.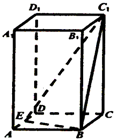 已知正四棱柱ABCD-A1B1C1D1的底面边长为2,侧棱长为底面边长的2倍,E点为AD的中点,则三棱锥D-BEC1的体积为( )
已知正四棱柱ABCD-A1B1C1D1的底面边长为2,侧棱长为底面边长的2倍,E点为AD的中点,则三棱锥D-BEC1的体积为( )
 已知正四棱柱ABCD-A1B1C1D1的底面边长为2,侧棱长为底面边长的2倍,E点为AD的中点,则三棱锥D-BEC1的体积为( )
已知正四棱柱ABCD-A1B1C1D1的底面边长为2,侧棱长为底面边长的2倍,E点为AD的中点,则三棱锥D-BEC1的体积为( )| A. | $\frac{8}{3}$ | B. | 4 | C. | $\frac{4}{3}$ | D. | 8 |
16.已知椭圆$\frac{x^2}{9}+\frac{y^2}{b^2}=1$(0<b<3),左、右焦点分别为F1、F2,过F1的直线交椭圆于 A,B两点,若|AF2|+|BF2|的最大值为8,则椭圆的离心率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{{\sqrt{2}}}{3}$ | C. | $\frac{{\sqrt{6}}}{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
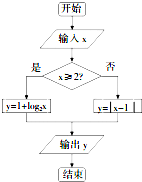 如图程序框图,当输出的任何一个确定的y值时恰好只对应输入唯一的x值,则这是输出的y值的范围是[0,+∞).
如图程序框图,当输出的任何一个确定的y值时恰好只对应输入唯一的x值,则这是输出的y值的范围是[0,+∞).