题目内容
8．已知集合A={x|log3（x2-2x）＞1}，B={x∈N|x＜5}，则（ ）| A． | A∩B=（3，5） | B． | A∪B=5 | C． | A∪B={x|x≤5} | D． | A∩B={4} |
分析 通过log3（x2-2x）＞1可得x＞3或x＜-1，计算即得结论．
解答 解：∵A={x|log3（x2-2x）＞1}，
∴A={x|x2-2x＞3}={x|x2-2x-3＞0}={x|x＞3或x＜-1}，
又∵B={x∈N|x＜5}，
∴A∩B={4}，
故选：D．
点评 本题考查集合的交运算，注意解题方法的积累，属于中档题．
练习册系列答案
小博士期末闯关100分系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
19．
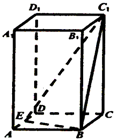已知正四棱柱ABCD-A1B1C1D1的底面边长为2，侧棱长为底面边长的2倍，E点为AD的中点，则三棱锥D-BEC1的体积为（ ）
已知正四棱柱ABCD-A1B1C1D1的底面边长为2，侧棱长为底面边长的2倍，E点为AD的中点，则三棱锥D-BEC1的体积为（ ）| A． | $\frac{8}{3}$ | B． | 4 | C． | $\frac{4}{3}$ | D． | 8 |
16．已知椭圆$\frac{x^2}{9}+\frac{y^2}{b^2}=1$（0＜b＜3），左、右焦点分别为F1、F2，过F1的直线交椭圆于 A，B两点，若|AF2|+|BF2|的最大值为8，则椭圆的离心率是（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{{\sqrt{2}}}{3}$ | C． | $\frac{{\sqrt{6}}}{3}$ | D． | $\frac{{\sqrt{3}}}{3}$ |
3．与双曲线C：$\frac{{x}^{2}}{12}-\frac{{y}^{2}}{4}$=1共焦点，且过点（0，3）的椭圆的离心率为（ ）
| A． | $\frac{2\sqrt{34}}{17}$ | B． | $\frac{\sqrt{6}}{3}$ | C． | $\frac{4\sqrt{7}}{7}$ | D． | $\frac{4}{5}$ |