题目内容
14.若椭圆M1:$\frac{{x}^{2}}{{a}_{1}^{2}}$+$\frac{{y}^{2}}{{b}_{1}^{2}}$=1(a1>b1>0)和椭圆M2:$\frac{{x}^{2}}{{a}_{2}^{2}}$+$\frac{{y}^{2}}{{b}_{2}^{2}}$=1(a2>b2>0)的长轴长相等,c1、c2分别为它们的半焦距,且b1>b2.给出下列五个命题,其中为真命题的是②④⑤(写出所有真命题的序号)①设椭圆的离心率为e,则e1>e2;②b12-b22=c22-c12;③b2c1>b1c2;
④设椭圆M1的焦点F1、F2,P1为椭圆M1上的任意一点,椭圆M2的焦点F3、F4,P2为椭圆M2上的任意一点,则∠F1P1F2和∠F3P2F4都取最大角时,∠F1P1F2<∠F3P2F4;
⑤若称椭圆上的点与焦点之间的线段之间的线段长度为焦半径,则椭圆M1的最短的焦半径比椭圆M2的最短的焦半径要长.
分析 利用椭圆M1:$\frac{{x}^{2}}{{a}_{1}^{2}}$+$\frac{{y}^{2}}{{b}_{1}^{2}}$=1(a1>b1>0)和椭圆M2:$\frac{{x}^{2}}{{a}_{2}^{2}}$+$\frac{{y}^{2}}{{b}_{2}^{2}}$=1(a2>b2>0)的长轴长相等,c1、c2分别为它们的半焦距,且b1>b2.对五个命题,分别进行判断,即可得出结论.
解答 解:①设椭圆的离心率为e,因为b1>b2,所以c1<c2,则e1<e2,故不正确;
②因为a1=a2,所以b12+c12=b22+c22,所以b12-b22=c22-c12,故正确;
③因为b1>b2,c1<c2,所以b2c1<b1c2,故不正确;
④设椭圆M1的焦点F1、F2,P1为椭圆M1上的任意一点,椭圆M2的焦点F3、F4,P2为椭圆M2上的任意一点,则因为b1>b2,c1<c2,所以∠F1P1F2和∠F3P2F4都取最大角时,∠F1P1F2<∠F3P2F4,故正确;
⑤若称椭圆上的点与焦点之间的线段之间的线段长度为焦半径,则椭圆M1的最短的焦半径a1-c1比椭圆M2的最短的焦半径a2-c2要长,故正确.
故答案为:②④⑤.
点评 本题考查椭圆的性质,考查命题真假判断,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
15.已知等差数列{an}中,a2+a6=16,则a4=( )
| A. | 7 | B. | 8 | C. | 9 | D. | 10 |
19.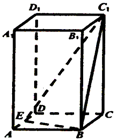 已知正四棱柱ABCD-A1B1C1D1的底面边长为2,侧棱长为底面边长的2倍,E点为AD的中点,则三棱锥D-BEC1的体积为( )
已知正四棱柱ABCD-A1B1C1D1的底面边长为2,侧棱长为底面边长的2倍,E点为AD的中点,则三棱锥D-BEC1的体积为( )
 已知正四棱柱ABCD-A1B1C1D1的底面边长为2,侧棱长为底面边长的2倍,E点为AD的中点,则三棱锥D-BEC1的体积为( )
已知正四棱柱ABCD-A1B1C1D1的底面边长为2,侧棱长为底面边长的2倍,E点为AD的中点,则三棱锥D-BEC1的体积为( )| A. | $\frac{8}{3}$ | B. | 4 | C. | $\frac{4}{3}$ | D. | 8 |
3.与双曲线C:$\frac{{x}^{2}}{12}-\frac{{y}^{2}}{4}$=1共焦点,且过点(0,3)的椭圆的离心率为( )
| A. | $\frac{2\sqrt{34}}{17}$ | B. | $\frac{\sqrt{6}}{3}$ | C. | $\frac{4\sqrt{7}}{7}$ | D. | $\frac{4}{5}$ |

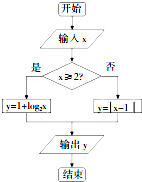 如图程序框图,当输出的任何一个确定的y值时恰好只对应输入唯一的x值,则这是输出的y值的范围是[0,+∞).
如图程序框图,当输出的任何一个确定的y值时恰好只对应输入唯一的x值,则这是输出的y值的范围是[0,+∞).