题目内容
1.在△ABC中,sin2A=sinBsinC,∠A=$\frac{π}{3}$,则∠B等于( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{4}$ | D. | $\frac{π}{3}$或$\frac{2π}{3}$ |
分析 利用三角形的内角和定理及诱导公式得到cosA=-cos(B+C),再利用两角和与差的余弦函数公式化简,把A的度数代入已知等式求出sinBsinC的值,代入计算求出cosBcosC的值,再利用两角和与差的余弦函数公式求出cos(B-C)的值,进而得到∠B=∠C,即可求出∠B的度数.
解答 解:∵在△ABC中,sin2A=sinBsinC,∠A=$\frac{π}{3}$,
∴cosA=-cos(B+C)=-cosBcosC+sinBsinC=-cosBcosC+sin2A=-cosBcosC+$\frac{3}{4}$=$\frac{1}{2}$,
∴cosBcosC=$\frac{1}{4}$,
∵sinBsinC=$\frac{3}{4}$,
∴cos(B-C)=cosBcosC+sinBsinC=1,即∠B-∠C=0,
∴∠B=∠C=$\frac{π}{3}$,
故选:B.
点评 此题考查了正弦定理,两角和与差的余弦函数公式,以及特殊角的三角函数值,熟练掌握正弦定理是解本题的关键.

练习册系列答案
相关题目
12.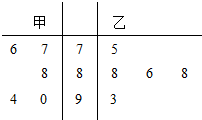 在“唱响内江”选拔赛中,甲、乙两位歌手的5次得分情况如茎叶图所示,记甲、乙两人的平均得分分别$\overline{{X}_{甲}}$、$\overline{{X}_{乙}}$,则下列判断正确的是( )
在“唱响内江”选拔赛中,甲、乙两位歌手的5次得分情况如茎叶图所示,记甲、乙两人的平均得分分别$\overline{{X}_{甲}}$、$\overline{{X}_{乙}}$,则下列判断正确的是( )
 在“唱响内江”选拔赛中,甲、乙两位歌手的5次得分情况如茎叶图所示,记甲、乙两人的平均得分分别$\overline{{X}_{甲}}$、$\overline{{X}_{乙}}$,则下列判断正确的是( )
在“唱响内江”选拔赛中,甲、乙两位歌手的5次得分情况如茎叶图所示,记甲、乙两人的平均得分分别$\overline{{X}_{甲}}$、$\overline{{X}_{乙}}$,则下列判断正确的是( )| A. | $\overline{{X}_{甲}}$<$\overline{{X}_{乙}}$,乙比甲成绩稳定 | B. | $\overline{{X}_{甲}}$<$\overline{{X}_{乙}}$,甲比乙成绩稳定 | ||
| C. | $\overline{{X}_{甲}}$>$\overline{{X}_{乙}}$,甲比乙成绩稳定 | D. | $\overline{{X}_{甲}}$>$\overline{{X}_{乙}}$,乙比甲成绩稳定 |
19.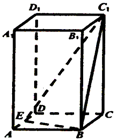 已知正四棱柱ABCD-A1B1C1D1的底面边长为2,侧棱长为底面边长的2倍,E点为AD的中点,则三棱锥D-BEC1的体积为( )
已知正四棱柱ABCD-A1B1C1D1的底面边长为2,侧棱长为底面边长的2倍,E点为AD的中点,则三棱锥D-BEC1的体积为( )
 已知正四棱柱ABCD-A1B1C1D1的底面边长为2,侧棱长为底面边长的2倍,E点为AD的中点,则三棱锥D-BEC1的体积为( )
已知正四棱柱ABCD-A1B1C1D1的底面边长为2,侧棱长为底面边长的2倍,E点为AD的中点,则三棱锥D-BEC1的体积为( )| A. | $\frac{8}{3}$ | B. | 4 | C. | $\frac{4}{3}$ | D. | 8 |

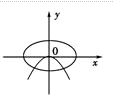

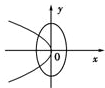

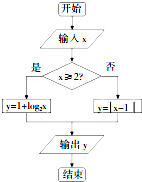 如图程序框图,当输出的任何一个确定的y值时恰好只对应输入唯一的x值,则这是输出的y值的范围是[0,+∞).
如图程序框图,当输出的任何一个确定的y值时恰好只对应输入唯一的x值,则这是输出的y值的范围是[0,+∞).