题目内容
7.“$\frac{{a}^{2}+{b}^{2}}{ab}$≤-2”是“a<0且b>0”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 可以通过移项求出不等式的解集,再根据充分必要条件进行判断.
解答 解:$\frac{{a}^{2}+{b}^{2}}{ab}$≤-2可得$\frac{{a}^{2}+{b}^{2}}{ab}$+2=$\frac{(a+b)^{2}}{ab}$≤0,即ab<0,即a>0,b<0,或a<0,b>0,
∴“$\frac{{a}^{2}+{b}^{2}}{ab}$≤-2”是“a<0且b>0”的必要不充分条件.
故选:B.
点评 此题主要考查充分必要条件的定义,以及不等式的求解,是一道基础题.

练习册系列答案
相关题目
20.下列四个命题中,正确的是( )
| A. | 若平面α∥平面β,直线m∥平面α,则m∥β | |
| B. | 若平面α⊥平面γ,且平面β⊥平面γ,则α∥β | |
| C. | 平面α⊥平面β,其α∩β=l,点A∈α,A∉l,若直线AB⊥l,则AB⊥β | |
| D. | 直线m,n为异面直线,且m⊥平面α,n⊥平面β,若m⊥n,则α⊥β |
12.在极坐标系中,已知△ABC的三个顶点的极坐标系分别为A(2,$\frac{π}{3}$)、B(2,π)、C(2,$\frac{5π}{3}$).
(1)判断△ABC的形状;
(2)求△ABC的面积.
(1)判断△ABC的形状;
(2)求△ABC的面积.
16.如图是函数y=2sin(ωx+ϕ)(ω>0)图象的一部分,则ω和ϕ为( )


| A. | ω=$\frac{11}{5}$,ϕ=-$\frac{5π}{6}$ | B. | ω=$\frac{7}{5}$,ϕ=-$\frac{π}{6}$ | C. | ω=$\frac{17}{5}$,ϕ=-$\frac{5π}{6}$ | D. | ω=$\frac{13}{5}$,ϕ=-$\frac{π}{6}$ |
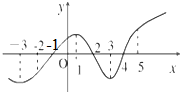 已知函数y=f(x)的导函数f′(x)的图象如图所示,则函数f(x)在区间[-3,5]上取得极大值时,x的取值为2.
已知函数y=f(x)的导函数f′(x)的图象如图所示,则函数f(x)在区间[-3,5]上取得极大值时,x的取值为2.