题目内容
1.函数y=ln|x-1|的图象与函数y=-cosπx(-2≤x≤4)的图象所有交点的横坐标之和等于( )| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
分析 根据函数的性质对称函数y=ln|x-1|的图象与函数y=-cosπx(-2≤x≤4)的图象关于x=1对称,
画出图象判断交点个数,利用对称性整体求解即可.
解答 解:∵y=ln|x|是偶函数,对称轴x=0,
∴函数y=ln|x-1|的图象的对称轴x=1,
∵函数y=-cosπx,
∴对称轴x=k,k∈z,
∴函数y=ln|x-1|的图象与函数y=-cosπx(-2≤x≤4)的图象关于x=1对称,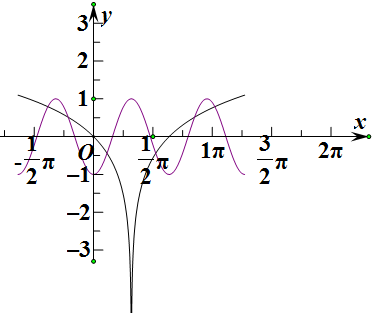
由图知,两个函数图象恰有6个交点,其横坐标分别为x1,x2,x3,与x1′,x2′,x3′,
可知:x1+x1′=2,x2$+{x}_{2}^{′}$=2,x3$+{x}_{3}^{′}$=2,
∴所有交点的横坐标之和等于6
故选:A.
点评 本题他考查对数函数与余弦函数的图象与性质,着重考查作图与分析、解决问题的能力,作图是难点,分析结论是关键,属于难题

练习册系列答案
相关题目
9.“a+b>0”是“任意的x∈[0,1],ax+b>0恒成立”的( )
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
10.若一个函数存在定义域和值域相同的区间,则称这个函数为这个区间上的一个“保城函数”,给出下列四个函数:
①f(x)=-x3;
②f(x)=3x;
③f(x)=sin$\frac{πx}{3}$;
④f(x)=2ln3x-3.
其中可以找到一个区间使其为保城函数的有( )
①f(x)=-x3;
②f(x)=3x;
③f(x)=sin$\frac{πx}{3}$;
④f(x)=2ln3x-3.
其中可以找到一个区间使其为保城函数的有( )
| A. | ①② | B. | ①③ | C. | ②③ | D. | ②④ |
7.“$\frac{{a}^{2}+{b}^{2}}{ab}$≤-2”是“a<0且b>0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
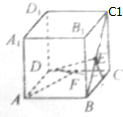 如图,在正方体ABCD-A1B1C1D1中,E、F分别是BC1,DC的中点.
如图,在正方体ABCD-A1B1C1D1中,E、F分别是BC1,DC的中点.