题目内容
20.下列四个命题中,正确的是( )| A. | 若平面α∥平面β,直线m∥平面α,则m∥β | |
| B. | 若平面α⊥平面γ,且平面β⊥平面γ,则α∥β | |
| C. | 平面α⊥平面β,其α∩β=l,点A∈α,A∉l,若直线AB⊥l,则AB⊥β | |
| D. | 直线m,n为异面直线,且m⊥平面α,n⊥平面β,若m⊥n,则α⊥β |
分析 根据平面与平面平行的性质进行判定,以及直线与平面位置关系的定义进行判定即可.
解答 解:因为平面α∥平面β,而直线m∥平面α
则当m在平面β内,原命题成立,
若m不在平面β内,则m一定与平面β平行;A错.
对于B,以正方体过同一顶点的三个面为例,确定其中一个面是β,另外两个面分别是α、γ,
可得α⊥β且β⊥γ,但α与γ不平行,因此B是假命题;
对于C,平面α⊥平面β,其α∩β=l,点A∈α,A∉l,若AB⊥l,则由平面与平面垂直的性质定理可知:AB⊥β,C正确.
对于D.直线m,n为异面直线,且m⊥平面α,n⊥平面β,若m⊥n,则α与β平行或相交.D错误.
故选:C
点评 本题主要考查了面面平行的性质,以及空间中直线与平面之间的位置关系,同时考查了空间想象能力,属于基础题.

练习册系列答案
相关题目
10.已知平面α与平面β相交于直线n,且不垂直,直线m?β,且m与n相交,点A∉α,l为过点A的一条动直线,那么下列情形可能出现的是( )
| A. | l∥m且l⊥α | B. | l⊥m且l⊥α | C. | l⊥m且l∥α | D. | l∥m且l∥α |
9.“a+b>0”是“任意的x∈[0,1],ax+b>0恒成立”的( )
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
7.“$\frac{{a}^{2}+{b}^{2}}{ab}$≤-2”是“a<0且b>0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
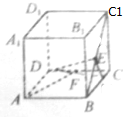 如图,在正方体ABCD-A1B1C1D1中,E、F分别是BC1,DC的中点.
如图,在正方体ABCD-A1B1C1D1中,E、F分别是BC1,DC的中点.