题目内容
【题目】如图所示的几何体中，四边形ABCD为梯形，AD∥BC，AB⊥平面BEC，EC⊥CB，已知BC=2AD=2AB=2． 
（1）证明：BD⊥平面DEC；
（2）若二面角A﹣ED﹣B的大小为30°，求EC的长度．
【答案】
（1）证明：∵AB⊥平面BEC，∴AB⊥EC，
又∵EC⊥BC，AB∩BC=B，∴EC⊥平面ABCD，
∵BD平面ABCD，∴EC⊥BD，
由题意知在梯形ABCD中，有BD=DC= 
，
∴BD2+DC2=BC2，∴BD⊥DC，
又EC∩CD=C，∴BD⊥平面DEC．
（2）解：如图，以B为原点，在平面BCE中过B作BC的垂线为x轴，
BC为y轴，BA为z轴，建立空间直角坐标系，
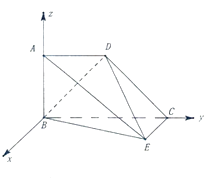
设 
=a＞0，则B（0，0，0），E（a，2，0），A（0，0，1），C（0，2，0），D（0，1，1），
=（0，1，0）， 
=（﹣a，﹣1，1），
设面AED的法向量为 
=（x，y，z），
则 
，令x=1，得 =（1，0，a），
设面BED的法向量为 
=（x1，y1，z1），
则 
，令x1=2，得 =（2，﹣a，a），
∵二面角A﹣ED﹣B的大小为30°，
∴cos30°= 
= 
= 
，解得a=1．（a=﹣1，舍），
∴EC=1．
【解析】（1）推导出AB⊥EC，EC⊥BC，从而EC⊥平面ABCD，进而EC⊥BD，由勾股定理得BD⊥DC，由此能证明BD⊥平面DEC．（2）以B为原点，在平面BCE中过B作BC的垂线为x轴，BC为y轴，BA为z轴，建立空间直角坐标系，利用向量法能求出EC．
【考点精析】掌握直线与平面垂直的判定是解答本题的根本，需要知道一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直；注意点：a)定理中的“两条相交直线”这一条件不可忽视；b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想．
