题目内容
【题目】已知函数f(x)=ax2﹣2ax+1+b(a>0)在区间[2,3]上的最大值为4,最小值为1.
(1)求a,b的值;
(2)设 ![]() ,若关于x的方程
,若关于x的方程 ![]() 在(﹣∞,0)∪(0,+∞)上有三个不同的实数解,求实数k的取值范围.
在(﹣∞,0)∪(0,+∞)上有三个不同的实数解,求实数k的取值范围.
【答案】
(1)解:f(x)=a(x﹣1)2+1+b﹣a.∵a>0,所以f(x)在[2,3]上为增函数,
故 ![]() ,即
,即 ![]()
解得a=1,b=0.
(2)解:g(x)= ![]() =x+
=x+ ![]() ,∴g(|2x﹣1|)=|2x﹣1|+
,∴g(|2x﹣1|)=|2x﹣1|+ ![]() ﹣2.
﹣2.
∵ ![]() ,∴
,∴ ![]() ,
,
即|2x﹣1|2﹣(2+3k)|2x﹣1|+(1+2k)=0,|2x﹣1|≠0.
令|2x﹣1|=t,则方程可化为t2﹣(2+3k)t+(1+2k)=0(t>0),
由方程 ![]() 在(﹣∞,0)∪(0,+∞)上有三个不同的实数解,
在(﹣∞,0)∪(0,+∞)上有三个不同的实数解,
结合t=|2x﹣1|的图象(如右图)可知,
方程t2﹣(2+3k)t+(1+2k)=0有两个根t1,t2,且0<t1<1<t2或0<t1<1,t2=1.
记h(t)=t2﹣(2+3k)t+(1+2k),则 ![]() 或
或 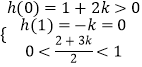 .
.
解得k>0.

【解析】(1)根据f(x)的开口方向和对称轴可知f(x)在[2,3]上是增函数,根据最值列出方程组解出a,b;(2)令|2x﹣1|=t,得到关于t的二次函数h(t),结合t=|2x﹣1|的函数图象可判断h(t)的零点分布情况,列出不等式组解出k的范围.
【考点精析】解答此题的关键在于理解二次函数的性质的相关知识,掌握当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减.
上递减.

练习册系列答案
相关题目