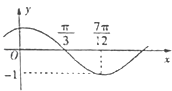
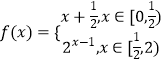题目内容
【题目】如图,AB是圆O的直径,PB是圆O的切线,过A点作AE∥OP交圆O于E点,PA交圆O于点F,连接PE. 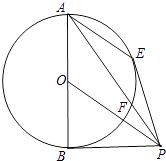
(1)求证:PE是圆O的切线;
(2)设AO=3,PB=4,求PF的长.
【答案】
(1)证明:连接OE,
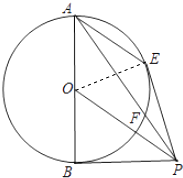
∵OA=OE,
∴∠OAE=∠OEA,
∵AE∥OP,
∴∠OAE=∠BOP,∠OEA=∠EOP,
∴∠BOP=∠EOP,又OB=OE,OP=OP,
∴△BOP≌△EOP,
∴∠OEP=∠OBP,
∵PB是圆O的切线,∴∠OBP=90°,
∴∠OEP=90°,
∴PE是圆O的切线.
(2)解:由(1)知△ABP 是直角三角形,
∵AB=2AO=6,PB=4,
∴PA= ![]() =2
=2 ![]() ,
,
∵PB是圆O的切线,
∴PB2=PFPA,
∴PF= ![]() =
= ![]() .
.
【解析】(1)连接OE,证明△BOP≌△EOP,可得∠OEP=∠OBP,根据PB是圆O的切线,证明PE是圆O的切线;(2)利用切割线定理求PF的长.

练习册系列答案
相关题目