题目内容
【题目】已知△DEF三边所在的直线分别为l1:x=-2,l2:x+![]() y-4=0,l3:x-
y-4=0,l3:x-![]() y-4=0,⊙C为△DEF的内切圆.
y-4=0,⊙C为△DEF的内切圆.
(1)求⊙C的方程;
(2)设⊙C与x轴交于A、B两点,点P在⊙C内,且满足![]() .记直线PA、PB的斜率分别为k1、k2,求k1 k2的取值范围.
.记直线PA、PB的斜率分别为k1、k2,求k1 k2的取值范围.
【答案】(1)x2+y2=4.(2)(-1,0]
【解析】
(1)解法一:设C(a,b),⊙C半径为r,则
![]() ,
,
结合点C(a,b)在△DEF内,可得![]() .
.
解得a=b=0,r=2.
∴⊙C的方程为x2+y2=4.
解法二:设C(a,b),⊙C半径为r.
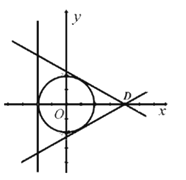
如图,由条件知,l2、l3的倾斜角分别为150°和30°,且它们关于x轴对称,同时l1⊥x轴.
因此,△DEF为正三角形.
∴点C在x轴上,且a=-2+r,b=0.
由l2、l3交x轴于点D(4,0),知△DEF的高为6.
∴![]() ,a=0.
,a=0.
∴⊙C的方程为x2+y2=4.
(2)由(1)知,C(0,0),A(-2,0),B(2,0).设P(x,y),则x2+y2<4.
∵![]() ,
,
∴![]() ,
,
化简得,x2-y2=2.
∴![]() .
.
由x2+y2<4,以及x2-y2=2,y2≥0,得2≤x2<3.
∴k1 k2∈(-1,0].
∴k1 k2的取值范围为(-1,0].

练习册系列答案
相关题目