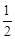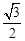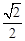题目内容
已知函数f(x)=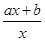 ex,a,b
ex,a,b R,且a>0.
R,且a>0.
⑴若a=2,b=1,求函数f(x)的极值;
⑵设g(x)=a(x-1)ex-f(x).
①当a=1时,对任意x (0,+∞),都有g(x)≥1成立,求b的最大值;
(0,+∞),都有g(x)≥1成立,求b的最大值;
②设g′(x)为g(x)的导函数.若存在x>1,使g(x)+g′(x)=0成立,求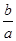 的取值范围.
的取值范围.
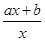 ex,a,b
ex,a,b R,且a>0.
R,且a>0.⑴若a=2,b=1,求函数f(x)的极值;
⑵设g(x)=a(x-1)ex-f(x).
①当a=1时,对任意x
 (0,+∞),都有g(x)≥1成立,求b的最大值;
(0,+∞),都有g(x)≥1成立,求b的最大值;②设g′(x)为g(x)的导函数.若存在x>1,使g(x)+g′(x)=0成立,求
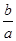 的取值范围.
的取值范围.⑴f (x)的极大值是f (-1)=e-1,f (x)的极小值是f (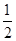 )=4
)=4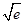 ;⑵① -1-e-1 ;②(-1,+∞).
;⑵① -1-e-1 ;②(-1,+∞).
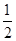 )=4
)=4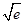 ;⑵① -1-e-1 ;②(-1,+∞).
;⑵① -1-e-1 ;②(-1,+∞).试题分析: ⑴由 a=2,b=1得,f (x)=(2+
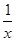 )ex, 定义域为(-∞,0)∪(0,+∞);从而可求得 f ′(x)=
)ex, 定义域为(-∞,0)∪(0,+∞);从而可求得 f ′(x)=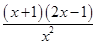 ex, 令f ′(x)=0,得x1=-1,x2=
ex, 令f ′(x)=0,得x1=-1,x2=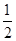 ,列表可求得f (x)的极值.
,列表可求得f (x)的极值.⑵①当a=1时,g (x)=(x-
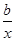 -2)ex,由已知得不等式g (x)≥1在x∈(0,+∞)上恒成立,即b≤x2-2x-
-2)ex,由已知得不等式g (x)≥1在x∈(0,+∞)上恒成立,即b≤x2-2x-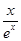 在x∈(0,+∞)上恒成立,从而b≤(x2-2x-
在x∈(0,+∞)上恒成立,从而b≤(x2-2x-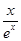 )min x∈(0,+∞),令h(x)=x2-2x-
)min x∈(0,+∞),令h(x)=x2-2x-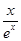 (x>0)利用函数导数求出h(x)的最小值即可.
(x>0)利用函数导数求出h(x)的最小值即可.②由于g (x)=(ax-
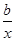 -2a)ex,所以g ′(x)=(
-2a)ex,所以g ′(x)=(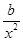 +ax-
+ax-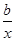 -a)ex; 由g (x)+g ′(x)=0,得(ax-
-a)ex; 由g (x)+g ′(x)=0,得(ax-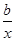 -2a)ex+(
-2a)ex+(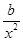 +ax-
+ax-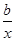 -a)ex=0,整理得2ax3-3ax2-2bx+b=0.
-a)ex=0,整理得2ax3-3ax2-2bx+b=0.存在x>1,使g (x)+g ′(x)=0成立,等价于存在x>1,2ax3-3ax2-2bx+b=0成立.
注意到a>0,所以
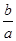 =
=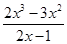 (x>1);设u(x)=
(x>1);设u(x)=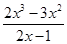 (x>1),则问题等价于
(x>1),则问题等价于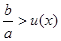 的最小值(或下确界),利用函数导数可判断u(x)在
的最小值(或下确界),利用函数导数可判断u(x)在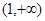 上的单调性可求得
上的单调性可求得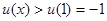 从而可得
从而可得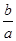 的取值范围为(-1,+∞).
的取值范围为(-1,+∞).试题解析:⑴当a=2,b=1时,f (x)=(2+
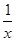 )ex,定义域为(-∞,0)∪(0,+∞).
)ex,定义域为(-∞,0)∪(0,+∞).所以f ′(x)=
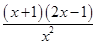 ex.令f ′(x)=0,得x1=-1,x2=
ex.令f ′(x)=0,得x1=-1,x2=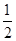 ,列表
,列表| x | (-∞,-1) | -1 | (-1,0) | (0,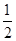 ) ) | 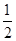 | (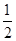 ,+∞) ,+∞) |
| f ′(x) | 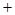 | 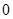 | - | - | 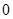 | 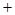 |
| f (x) | ↗ | 极大值 | ↘ | ↘ | 极小值 | ↗ |
由表知f (x)的极大值是f (-1)=e-1,f (x)的极小值是f (
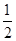 )=4
)=4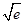 .
.⑵① 因为g (x)=(ax-a)ex-f (x)=(ax-
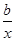 -2a)ex,当a=1时,g (x)=(x-
-2a)ex,当a=1时,g (x)=(x-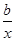 -2)ex.
-2)ex.因为g (x)≥1在x∈(0,+∞)上恒成立,所以b≤x2-2x-
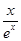 在x∈(0,+∞)上恒成立.
在x∈(0,+∞)上恒成立.记h(x)=x2-2x-
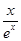 (x>0),则h′(x)=
(x>0),则h′(x)=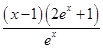 .
.当0<x<1时,h′(x)<0,h(x)在(0,1)上是减函数;
当x>1时,h′(x)>0,h(x)在(1,+∞)上是增函数.
所以h(x)min=h(1)=-1-e-1.所以b的最大值为-1-e-1.
②因为g (x)=(ax-
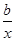 -2a)ex,所以g ′(x)=(
-2a)ex,所以g ′(x)=(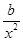 +ax-
+ax-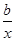 -a)ex.
-a)ex.由g (x)+g ′(x)=0,得(ax-
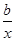 -2a)ex+(
-2a)ex+(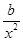 +ax-
+ax-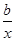 -a)ex=0,整理得2ax3-3ax2-2bx+b=0.
-a)ex=0,整理得2ax3-3ax2-2bx+b=0.存在x>1,使g (x)+g ′(x)=0成立,等价于存在x>1,2ax3-3ax2-2bx+b=0成立.
因为a>0,所以
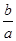 =
=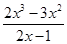 .设u(x)=
.设u(x)=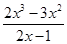 (x>1),则u′(x)=
(x>1),则u′(x)=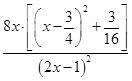 .
.因为x>1,u′(x)>0恒成立,所以u(x)在(1,+∞)是增函数,所以u(x)>u(1)=-1,
所以
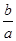 >-1,即
>-1,即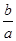 的取值范围为(-1,+∞).
的取值范围为(-1,+∞).
练习册系列答案
相关题目
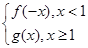 ,对任意给定的正实数a,曲线y=F(x)上是否存在两点P,Q,使得△POQ是以O(O为坐标原点)为直角顶点的直角三角形,而且此三角形斜边中点在y轴上?请说明理由.
,对任意给定的正实数a,曲线y=F(x)上是否存在两点P,Q,使得△POQ是以O(O为坐标原点)为直角顶点的直角三角形,而且此三角形斜边中点在y轴上?请说明理由.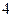 的圆的矩形的面积的最大值是( )
的圆的矩形的面积的最大值是( )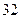
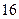
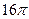
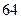
 的导函数
的导函数 的图像如图所示,那么
的图像如图所示,那么

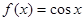 ,
,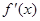 是它的导函数,则
是它的导函数,则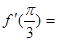 。
。 的图象上一点
的图象上一点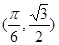 处的切线的斜率为( )
处的切线的斜率为( )