题目内容
已知函数f(x)=ax2-(a+2)x+ln x.
(1)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)当a>0时,若f(x)在区间[1,e]上的最小值为-2,求a的取值范围;
(3)若对任意x1,x2∈(0,+∞),x1<x2,且f(x1)+2x1<f(x2)+2x2恒成立,求a的取值范围.
(1)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)当a>0时,若f(x)在区间[1,e]上的最小值为-2,求a的取值范围;
(3)若对任意x1,x2∈(0,+∞),x1<x2,且f(x1)+2x1<f(x2)+2x2恒成立,求a的取值范围.
(1)y=-2.
(2)[1,+∞)
(3)[0,8]
(2)[1,+∞)
(3)[0,8]
(1)当a=1时,f(x)=x2-3x+ln x,f′(x)=2x-3+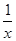 .
.
因为f′(1)=0,f(1)=-2.
所以切线方程是y=-2.
(2)函数f(x)=ax2-(a+2)x+ln x的定义域是(0,+∞).
当a>0时,f′(x)=2ax-(a+2)+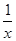 =
=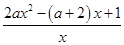 (x>0),
(x>0),
令f′(x)=0,即f′(x)=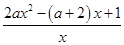
=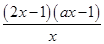 =0,
=0,
所以x=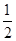 或x=
或x=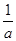 .
.
当0<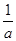 ≤1,即a≥1时,f(x)在[1,e]上单调递增,
≤1,即a≥1时,f(x)在[1,e]上单调递增,
所以f(x)在[1,e]上的最小值是f(1)=-2;
当1<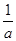 <e时,f(x)在[1,e]上的最小值是f
<e时,f(x)在[1,e]上的最小值是f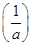 <f(1)=-2,不合题意;
<f(1)=-2,不合题意;
当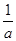 ≥e时,f(x)在(1,e)上单调递减,
≥e时,f(x)在(1,e)上单调递减,
所以f(x)在[1,e]上的最小值是f(e)<f(1)=-2,不合题意.
综上a的取值范围是[1,+∞).
(3)设g(x)=f(x)+2x,则g(x)=ax2-ax+ln x,
只要g(x)在(0,+∞)上单调递增即可.
而g′(x)=2ax-a+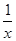 =
=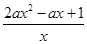 ,
,
当a=0时,g′(x)=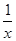 >0,此时g(x)在(0,+∞)上单调递增;
>0,此时g(x)在(0,+∞)上单调递增;
当a≠0时,只需g′(x)≥0在(0,+∞)上恒成立,因为x∈(0,+∞),只要2ax2-ax+1≥0,则需要a>0,
对于函数y=2ax2-ax+1,过定点(0,1),对称轴x=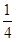 >0,只需Δ=a2-8a≤0,
>0,只需Δ=a2-8a≤0,
即0<a≤8.
综上a的取值范围是[0,8].
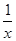 .
.因为f′(1)=0,f(1)=-2.
所以切线方程是y=-2.
(2)函数f(x)=ax2-(a+2)x+ln x的定义域是(0,+∞).
当a>0时,f′(x)=2ax-(a+2)+
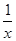 =
=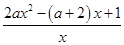 (x>0),
(x>0),令f′(x)=0,即f′(x)=
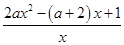
=
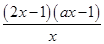 =0,
=0,所以x=
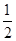 或x=
或x=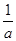 .
.当0<
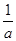 ≤1,即a≥1时,f(x)在[1,e]上单调递增,
≤1,即a≥1时,f(x)在[1,e]上单调递增,所以f(x)在[1,e]上的最小值是f(1)=-2;
当1<
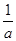 <e时,f(x)在[1,e]上的最小值是f
<e时,f(x)在[1,e]上的最小值是f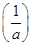 <f(1)=-2,不合题意;
<f(1)=-2,不合题意;当
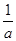 ≥e时,f(x)在(1,e)上单调递减,
≥e时,f(x)在(1,e)上单调递减,所以f(x)在[1,e]上的最小值是f(e)<f(1)=-2,不合题意.
综上a的取值范围是[1,+∞).
(3)设g(x)=f(x)+2x,则g(x)=ax2-ax+ln x,
只要g(x)在(0,+∞)上单调递增即可.
而g′(x)=2ax-a+
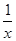 =
=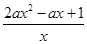 ,
,当a=0时,g′(x)=
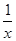 >0,此时g(x)在(0,+∞)上单调递增;
>0,此时g(x)在(0,+∞)上单调递增;当a≠0时,只需g′(x)≥0在(0,+∞)上恒成立,因为x∈(0,+∞),只要2ax2-ax+1≥0,则需要a>0,
对于函数y=2ax2-ax+1,过定点(0,1),对称轴x=
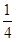 >0,只需Δ=a2-8a≤0,
>0,只需Δ=a2-8a≤0,即0<a≤8.
综上a的取值范围是[0,8].

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
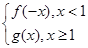 ,对任意给定的正实数a,曲线y=F(x)上是否存在两点P,Q,使得△POQ是以O(O为坐标原点)为直角顶点的直角三角形,而且此三角形斜边中点在y轴上?请说明理由.
,对任意给定的正实数a,曲线y=F(x)上是否存在两点P,Q,使得△POQ是以O(O为坐标原点)为直角顶点的直角三角形,而且此三角形斜边中点在y轴上?请说明理由.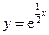 在点
在点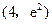 处的切线与坐标轴所围三角形的面积为 。
处的切线与坐标轴所围三角形的面积为 。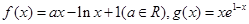 。
。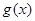 在区间
在区间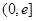 上的值域;
上的值域;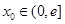 ,在区间
,在区间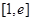 上都存在两个不同的
上都存在两个不同的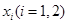 ,使得
,使得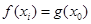 成立.若存在,求出a的取值范围;若不存在,请说明理由.
成立.若存在,求出a的取值范围;若不存在,请说明理由.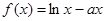 ,
, ,其中
,其中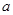 为实数,若
为实数,若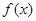 在
在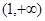 上是单调减函数,且
上是单调减函数,且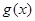 在
在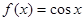 ,
,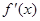 是它的导函数,则
是它的导函数,则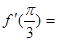 。
。 的图象上一点
的图象上一点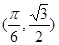 处的切线的斜率为( )
处的切线的斜率为( )