题目内容
13．
如图是利用斜二测画法画出的△ABO的直观图，已知O′B′=4，且△ABO的面积为16，过A′作A′C′⊥x′轴，则A′C′的长为（ ）| A． | $2\sqrt{2}$ | B． | $\sqrt{2}$ | C． | $16\sqrt{2}$ | D． | 1 |
分析 利用面积公式，求出直观图的高，求出A′B′，然后求出A'O'的长．
解答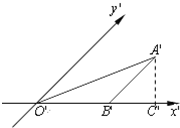 
解：因为A'B'∥y'轴，所以在△ABC中，AB⊥OB，又三角形的面积为16，
所以$\frac{1}{2}$AB•OB=16．∴AB=8，
所以A'B'=4．如图作A′D⊥O′B′于D，
所以B′C′=A′C′，
所以A'C'的长为：4•sin45°=2$\sqrt{2}$．
故选：A．
点评 本题考查平面图形与直观图的关系，注意斜二测画法中的线线关系以及角的关系，考查计算能力．
练习册系列答案
相关题目
