题目内容
已知定义域为R的函数f(x)=
是奇函数.
(1)求a,b的值;
(2)利用定义判断函数y=f(x)的单调性;
(3)若对任意t∈[0,1],不等式f(2t2+kt)+f(k-t2)>0恒成立,求实数k的取值范围.
| 2x-b |
| 2x+a |
(1)求a,b的值;
(2)利用定义判断函数y=f(x)的单调性;
(3)若对任意t∈[0,1],不等式f(2t2+kt)+f(k-t2)>0恒成立,求实数k的取值范围.
(1)∵f(x)为R上的奇函数,
∴f(0)=0,即
=0,可得b=1
又∵f(-1)=-f(1),即
=-
,解之得a=1,
经检验当a=1且b=1时,f(x)=
满足f(-x)=-f(x)是奇函数,
(2)由(1)得f(x)=
,任取实数x1、x2,且x1<x2
则f(x1)-f(x2)=
-
=
=
,
∵x1<x2,可得2x1-2x2<0,
∴f(x1)-f(x2)<0,即f(x1)<f(x2),
函数f(x)在(-∞,+∞)上为增函数;
(3)根据(1)(2)知,函数f(x)是奇函数且在(-∞,+∞)上为增函数.
∴不等式f(2t2+kt)+f(k-t2)>0对任意t∈[0,1]恒成立,
即f(2t2+kt)>-f(k-t2)=f(t2-k),
∴2t2+kt>t2-k对任意t∈[0,1]都成立.
即t2+kt+k>0,变量分离得k>-
对任意t∈[0,1]都成立,
设y=-
,则y′=
=
=
<0,
∴y=-
在[0,1]上递减,则函数的最大值是0,
综上得,k>0,
故实数k的取值范围是:k>0.
∴f(0)=0,即
| 1-b |
| 1+a |
又∵f(-1)=-f(1),即
| 2-1-1 |
| 2-1+a |
| 2-1 |
| 2+a |
经检验当a=1且b=1时,f(x)=
| 2x-1 |
| 2x+1 |
(2)由(1)得f(x)=
| 2x-1 |
| 2x+1 |
则f(x1)-f(x2)=
| 2x1-1 |
| 2x1+1 |
| 2x2-1 |
| 2x2+1 |
| (2x1-1)(2x2+1)-(2x2-1)(2x1+1) |
| (2x1+1)(2x2+1) |
=
| 2(2x1-2x2) |
| (2x1+1)(2x2+1) |
∵x1<x2,可得2x1-2x2<0,
∴f(x1)-f(x2)<0,即f(x1)<f(x2),
函数f(x)在(-∞,+∞)上为增函数;
(3)根据(1)(2)知,函数f(x)是奇函数且在(-∞,+∞)上为增函数.
∴不等式f(2t2+kt)+f(k-t2)>0对任意t∈[0,1]恒成立,
即f(2t2+kt)>-f(k-t2)=f(t2-k),
∴2t2+kt>t2-k对任意t∈[0,1]都成立.
即t2+kt+k>0,变量分离得k>-
| t2 |
| t+1 |
设y=-
| t2 |
| t+1 |
| (-t2)′(t+1)-(-t2)(t+1)′ |
| (t+1)2 |
=
| -2t(t+1)+t2 |
| (t+1)2 |
| -t2-2t |
| (t+1)2 |
∴y=-
| t2 |
| t+1 |
综上得,k>0,
故实数k的取值范围是:k>0.

练习册系列答案
相关题目
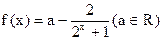 为奇函数(Ⅰ)求
为奇函数(Ⅰ)求 的值;(Ⅱ)用函数单调性定义及指数函数性质证明:
的值;(Ⅱ)用函数单调性定义及指数函数性质证明: 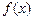 在
在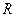 上是增函数。
上是增函数。