题目内容
(本题12分)对于函数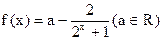 为奇函数(Ⅰ)求
为奇函数(Ⅰ)求 的值;(Ⅱ)用函数单调性定义及指数函数性质证明:
的值;(Ⅱ)用函数单调性定义及指数函数性质证明: 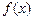 在
在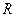 上是增函数。
上是增函数。
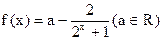 为奇函数(Ⅰ)求
为奇函数(Ⅰ)求 的值;(Ⅱ)用函数单调性定义及指数函数性质证明:
的值;(Ⅱ)用函数单调性定义及指数函数性质证明: 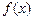 在
在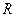 上是增函数。
上是增函数。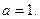
解:(Ⅰ)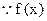 为奇函数,
为奇函数,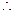
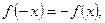 即
即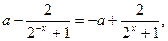
解得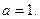 ………4分
………4分
(Ⅱ)证明: 由(Ⅰ)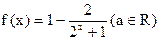 ,在
,在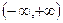 上任取
上任取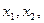 且
且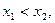 则
则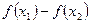
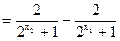
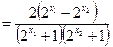 ,
,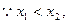
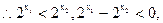
 …………8分
…………8分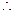
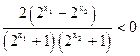 ,即
,即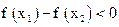
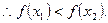
 在
在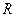 上单调递增. 12分
上单调递增. 12分
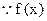 为奇函数,
为奇函数,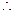
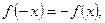 即
即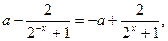
解得
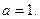 ………4分
………4分 (Ⅱ)证明: 由(Ⅰ)
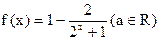 ,在
,在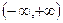 上任取
上任取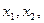 且
且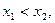 则
则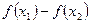
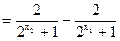
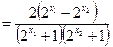 ,
,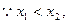
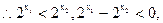
 …………8分
…………8分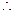
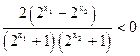 ,即
,即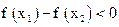
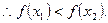
 在
在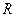 上单调递增. 12分
上单调递增. 12分
练习册系列答案
相关题目
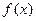 的定义域为R,若
的定义域为R,若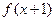 与
与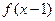 都是奇函数,则( )
都是奇函数,则( ) 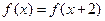
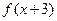 是奇函数
是奇函数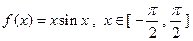 ,若
,若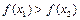 ,则下列不等式必定成立的是
,则下列不等式必定成立的是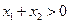
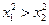
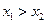
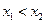
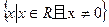 又f(x)在
又f(x)在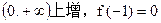 ,则f(x)>0的解集是( )
,则f(x)>0的解集是( )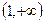 B (0,1) C
B (0,1) C 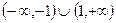 D
D 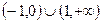
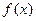 是
是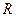 上的奇函数,且当
上的奇函数,且当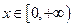 时,
时,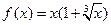 ,则当
,则当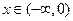 时
时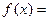 _____________________。
_____________________。