题目内容
2.已知cos($\frac{π}{4}$+x)=$\frac{3}{5}$,$\frac{17π}{12}$$<x<\frac{7π}{4}$.(Ⅰ)求sin2x的值.
(Ⅱ)求tanx的值.
分析 (Ⅰ)由诱导公式可求cos2($\frac{π}{4}$+x)=-sin2x,又利用二倍角公式可得cos2($\frac{π}{4}$+x)=2cos2($\frac{π}{4}$+x)-1=-$\frac{7}{25}$,即可解得sin2x的值.
(Ⅱ)由已知可求范围$\frac{5π}{3}<x+\frac{π}{4}<2π$,利用同角三角函数关系式可求sin($\frac{π}{4}$+x),可得tan($\frac{π}{4}$+x)=$\frac{sin(\frac{π}{4}+x)}{cos(\frac{π}{4}+x)}$=$\frac{1+tanx}{1-tanx}$=-$\frac{4}{3}$,即可得解.
解答 解:(Ⅰ)∵cos2($\frac{π}{4}$+x)=cos($\frac{π}{2}$+2x)=-sin2x,
又cos2($\frac{π}{4}$+x)=2cos2($\frac{π}{4}$+x)-1=2×$\frac{9}{25}-1$=-$\frac{7}{25}$.
∴sin2x=$\frac{7}{25}$.
(Ⅱ)∵$\frac{17π}{12}$$<x<\frac{7π}{4}$.
∴$\frac{5π}{3}<x+\frac{π}{4}<2π$,
∴sin($\frac{π}{4}$+x)=-$\sqrt{1-co{s}^{2}(\frac{π}{4}+x)}$=-$\frac{4}{5}$,
∴tan($\frac{π}{4}$+x)=$\frac{sin(\frac{π}{4}+x)}{cos(\frac{π}{4}+x)}$=$\frac{1+tanx}{1-tanx}$=-$\frac{4}{3}$,
∴tanx=7.
点评 本题主要考查了诱导公式,二倍角公式,同角三角函数关系式的应用,属于基础题.

 名师点拨卷系列答案
名师点拨卷系列答案| A. | 20 | B. | 16 | C. | -18 | D. | -17 |
| A. | ①② | B. | ③④ | C. | ①②④ | D. | ①②③④ |
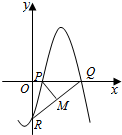 如图,函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|≤$\frac{π}{2}$)与坐标轴的三个交点P、Q、R满足P(1,0),M(2,-2)为线段QR的中点,则A=( )
如图,函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,|φ|≤$\frac{π}{2}$)与坐标轴的三个交点P、Q、R满足P(1,0),M(2,-2)为线段QR的中点,则A=( )| A. | 2$\sqrt{3}$ | B. | $\frac{7\sqrt{3}}{3}$ | C. | $\frac{8\sqrt{3}}{3}$ | D. | 4$\sqrt{3}$ |