题目内容
14.设向量$\overrightarrow{a}$=(-1,4),$\overrightarrow{b}$=(2,x),若($\overrightarrow{a}+\overrightarrow{b}$)$∥(\overrightarrow{a}-\overrightarrow{b})$,则x等于( )| A. | $\frac{1}{2}$ | B. | 2 | C. | -2 | D. | -8 |
分析 根据两向量平行的坐标表示,列出方程组,求出x的值即可.
解答 解:∵向量$\overrightarrow{a}$=(-1,4),$\overrightarrow{b}$=(2,x),
∴($\overrightarrow{a}+\overrightarrow{b}$)=(1,4+x),∴($\overrightarrow{a}$$-\overrightarrow{b}$)=(-3,4-x),
∵($\overrightarrow{a}+\overrightarrow{b}$)$∥(\overrightarrow{a}-\overrightarrow{b})$,
∴4-x=-3(4+x),
解得x=-8,
故选:D.
点评 本题考查了平面向量平行的坐标表示及其应用问题,是基础题目.

练习册系列答案
相关题目
4.用数学归纳法证明1+$\frac{1}{2}+\frac{1}{3}+…$+$\frac{1}{{2}^{n}-1}<n$(n∈N且n>1),第二步证明中从“k到k+1”时,左端增加的项数是( )
| A. | 2k+1 | B. | 2k-1 | C. | 2k | D. | 2k-1 |
5.若随机变量X~N(1,σ2),且P(X>2)=0.3,则P(X≥0)等于( )
| A. | 0.7 | B. | 0.4 | C. | 0.8 | D. | 0.6 |
19.设x∈(0,$\frac{π}{2}$),lgsin2x-lgsinx=lg$\frac{1}{2}$,则tanx等于( )
| A. | $\sqrt{2}$ | B. | 2 | C. | $\sqrt{15}$ | D. | 5 |
4.已知sin(x+$\frac{π}{6}$)=$\frac{1}{4}$,则sin($\frac{5π}{6}$-x)+sin2($\frac{π}{3}$-x)的值为( )
| A. | -$\frac{3}{16}$ | B. | $\frac{5}{16}$ | C. | $\frac{15}{16}$ | D. | $\frac{19}{16}$ |
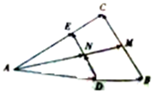 如图所示,在△ABC中,$\overrightarrow{AD}$=$\frac{2}{3}\overrightarrow{AB}$,DE∥BC交AC于E,AM是BC边上的中线,交DE于N.
如图所示,在△ABC中,$\overrightarrow{AD}$=$\frac{2}{3}\overrightarrow{AB}$,DE∥BC交AC于E,AM是BC边上的中线,交DE于N.