题目内容
【题目】已知f（x）= 
x3﹣2ax2﹣3x（a∈R）． （Ⅰ）若f（x）在区间（﹣1，1）内为减函数，求实数a的取值范围；
（Ⅱ）对于实数a的不同取值，试讨论y=f（x）在（﹣1，1）内的极值点的个数．
【答案】解：（Ⅰ）对函数g（x）求导得，f'（x）=2x2﹣4ax﹣3， ∵f（x）在区间（﹣1，1）内为减函数，
∴f'（x）≤0在x∈（﹣1，1）上恒成立，
结合二次函数的图象和性质，
问题等价为：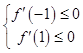 
，即 
，
解得﹣ 
≤a≤ ，
∴实数a的取值范围为[﹣ ， ]，
（Ⅱ）当a＜﹣ 时，f′（﹣1）=4a﹣1＜0，f′（1）=﹣4a﹣1＞0
∴f（x）在（﹣1，1）内有且只有一个极小值点，
当a＞ 时，f′（﹣1）=4a﹣1＞0，f′（1）=﹣4a﹣1＜0，
∴f（x）在（﹣1，1）内有且只有一个极大值点，
当﹣ ≤a≤ 时，由（Ⅰ）可知在区间（﹣1，1）上为减函数，
∴f（x）在区间（﹣1，1）内没有极值点．
综上可知，当a＜﹣ 或a＞ 时，函数在区间（﹣1，1）内的极值点个数为1；当﹣ ≤a≤ 时，在区间（﹣1，1）内的极值点个数为0
【解析】（Ⅰ）先求出导函数，根据题意问题等价为g'（x）≤0在x∈（﹣1，1）上恒成立，再根据二次函数的性质转化为： 
，解出即可，（Ⅱ）分类讨论．利用导数的正负，即可得出y=f（x）在（﹣1，1）内的极值点的个数．
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识，掌握一般的,函数的单调性与其导数的正负有如下关系： 在某个区间
内，(1)如果
，那么函数
在这个区间单调递增；(2)如果
，那么函数
在这个区间单调递减，以及对函数的极值与导数的理解，了解求函数的极值的方法是:（1）如果在
附近的左侧,右侧,那么
是极大值（2）如果在附近的左侧,右侧
,那么
是极小值．
