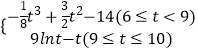题目内容
【题目】已知f(x)=xlnx,g(x)=﹣x2+ax﹣3. (Ⅰ)求函数f(x)在[t,t+1](t>0)上的最小值;
(Ⅱ)对一切x∈(0,+∞),2f(x)≥g(x)恒成立,求实数a的取值范围;
(Ⅲ)证明:对一切x∈(0,+∞),都有lnx> ![]() ﹣
﹣ ![]() 成立.
成立.
【答案】解:(Ⅰ)∵f′(x)=lnx+1, 当x∈(0, ![]() ),f′(x)<0,f(x)单调递减,当x∈(
),f′(x)<0,f(x)单调递减,当x∈( ![]() ,+∞),f′(x)>0,f(x)单调递增,
,+∞),f′(x)>0,f(x)单调递增,
① ![]() ,即0<t<
,即0<t< ![]() 时,f(x)min=
时,f(x)min= ![]() ,f(x)min=f(t)=tlnt
,f(x)min=f(t)=tlnt
② ![]() ,即t
,即t ![]() 时,f(x)在[t,t+1]上单调递增,f(x)min=f(t)=tlnt,
时,f(x)在[t,t+1]上单调递增,f(x)min=f(t)=tlnt,
∴ 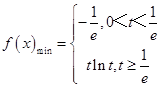
(Ⅱ)2xlnx≥﹣x2+ax﹣3,则 ![]() ,
,
设h(x)=2lnx+x+ ![]() ,x>0,则h′(x)=
,x>0,则h′(x)= ![]() ,
,
①x∈(0,1),h′(x)<0,h(x)单调递减,
②x∈(1,+∞),h′(x)>0,h(x)单调递增,
∴h(x)min=h(1)=4,对一切x∈(0,+∞),2f(x)≥g(x)恒成立,
∴a≤4.
(Ⅲ)问题等价于证明xlnx> ![]() ,
,
由(Ⅰ)可知f(x)=xlnx,(x∈(0,+∞))的最小值是- ![]() ,当且仅当x=
,当且仅当x= ![]() 时取到,
时取到,
设m(x)=xlnx> ![]() ,则
,则 ![]() ,
,
易知 ![]() ,当且仅当x=1时取到,
,当且仅当x=1时取到,
从而对一切x∈(0,+∞),都有都有lnx> ![]() ﹣
﹣ ![]() 成立
成立
【解析】(Ⅰ)求函数f(x)在某区间的最小值,先求该函数的导函数,再判断单调性,因为t是参数,要进行分类讨论;(Ⅱ)求实数a的取值范围,2f(x)≥g(x)恒成立,就是求函数的最值问题,(Ⅲ)本题设m(x)=xlnx> ![]() ,也是求m(x)=xlnx的最值问题.
,也是求m(x)=xlnx的最值问题.
【考点精析】本题主要考查了函数的最大(小)值与导数的相关知识点,需要掌握求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.
比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.

 金钥匙试卷系列答案
金钥匙试卷系列答案【题目】为了引导居民合理用电,国家决定实行合理的阶梯电价,居民用电原则上以住宅为单位(一套住宅为一户).
阶梯级别 | 第一阶梯 | 第二阶梯 | 第三阶梯 |
月用电范围(度) | (0,210] | (210,400] |
|
某市随机抽取10户同一个月的用电情况,得到统计表如下:
居民用电户编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
用电量(度) | 53 | 86 | 90 | 124 | 132 | 200 | 215 | 225 | 300 | 410 |
若规定第一阶梯电价每度0.5元,第二阶梯超出第一阶梯的部分每度0.6元,第三阶梯超出第二阶梯的部分每度0.8元,试计算A居民用电户用电410度时应电费多少元?
现要在这10户家庭中任意选取3户,求取到第二阶梯电量的户数的分布列与期望;
以表中抽到的10户作为样本估计全市的居民用电,现从全市中依次抽取10户,若抽到![]() 户用电量为第一阶梯的可能性最大,求
户用电量为第一阶梯的可能性最大,求![]() 的值.
的值.