题目内容
【题目】以边长为![]() 的正三角形
的正三角形![]() 的顶点
的顶点![]() 为坐标原点,另外两个顶点在抛物线
为坐标原点,另外两个顶点在抛物线![]() 上,过抛物线
上,过抛物线![]() 的焦点
的焦点![]() 的直线
的直线![]() 过交拋物线
过交拋物线![]() 于
于![]() 两点.
两点.
(1)求抛物线![]() 的方程;
的方程;
(2)求证: ![]() 为定值;
为定值;
(3)求线段![]() 的中点的轨迹方程.
的中点的轨迹方程.
【答案】(1)![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]()
【解析】试题分析:
(1)由题意结合几何关系列方程组可求得![]() ,则抛物线
,则抛物线![]() 的方程为
的方程为![]() .
.
(2)联立直线与抛物线的方程,利用韦达定理结合平面向量数量积的坐标运算计算可得![]() 为定值
为定值![]() ;
;
(3) 设线段![]() 的中点为
的中点为![]() ,则
,则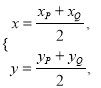 消去参数可得中点的轨迹方程为
消去参数可得中点的轨迹方程为![]() .
.
试题解析:
(1)因为正三角形和抛物线都是轴对称图形,且三角形的一个顶点扣抛物线的顶点重合,所以,三角形的顶点![]() 关于
关于![]() 轴对称,如图所示.
轴对称,如图所示.
由 可得
可得![]() ,
,
∵![]() ,∴
,∴![]() .
.
∴抛物线![]() 的方程为
的方程为![]() .
.

(2)易知抛物线![]() :
: ![]() 的焦点
的焦点![]() ,设直线
,设直线![]() ,并设点
,并设点![]() .
.
由![]() 可得
可得![]() ,∴
,∴![]()
∴![]() ,
,
∵![]() ,∴
,∴ ![]() .
.
(3)设线段![]() 的中点为
的中点为![]() ,
,
则
消去![]() 得线段
得线段![]() 的中点为
的中点为![]() 的轨迹方程为
的轨迹方程为![]() .
.

练习册系列答案
相关题目