题目内容
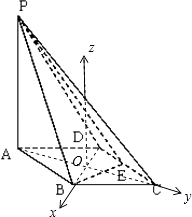
【题目】如图所示,四棱锥P﹣ABCD的底面ABCD是边长为1的菱形,∠BCD=60°,E是CD的中点,PA⊥底面ABCD,PA=2. (Ⅰ)证明:平面PBE⊥平面PAB;
(Ⅱ)求平面PAD和平面PBE所成二面角(锐角)的余弦值.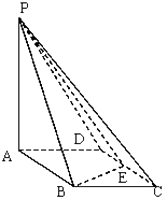
【答案】证明:(I)连接BD, ∵四边形ABCD是菱形,∠BCD=60°,
∴△BCD是等边三角形,
∵E是CD的中点,∴BE⊥CD,
∵CD∥AB,∴BE⊥AB.
∵PA⊥平面ABCD,BE平面ABCD,
∴PA⊥BE,又PA平面PAB,AB平面PAB,PA∩AB=A,
∴BE⊥平面PAB,又BE平面PBE,
∴平面PBE⊥平面PAB.
(II)设AC∩BD=O,以OB所在直线为x轴,以OC所在直线为y轴,
以平面ABCD过O的垂线为z轴建立如图所示的空间直角坐标系,
则A(0,﹣ ![]() ,0),B(
,0),B( ![]() ,0,0),C(0,
,0,0),C(0, ![]() ,0),D(﹣
,0),D(﹣ ![]() ,0,0),
,0,0),
P(0,﹣ ![]() ,2),E(﹣
,2),E(﹣ ![]() ,
, ![]() ,0),
,0),
∴ ![]() =(0,0,2),
=(0,0,2), ![]() =(﹣
=(﹣ ![]() ,
, ![]() ,0),
,0), ![]() =(﹣
=(﹣ ![]() ,
, ![]() ,0),
,0), ![]() =(﹣
=(﹣ ![]() ,﹣
,﹣ ![]() ,2).
,2).
设平面PAD的法向量为 ![]() =(x1 , y1 , z1),平面PBE的法向量为
=(x1 , y1 , z1),平面PBE的法向量为 ![]() =(x2 , y2 , z2),
=(x2 , y2 , z2),
则 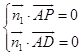 ,
, 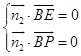 .
.
∴ 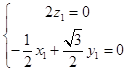 ,
, 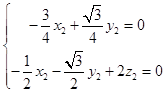 .
.
令x1= ![]() 得
得 ![]() =(
=( ![]() ,1,0),令x2=1得
,1,0),令x2=1得 ![]() =(1,
=(1, ![]() ,1).
,1).
∴cos< ![]() ,
, ![]() >=
>= 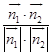 =
= ![]() =
= ![]() .
.
∵平面PAD和平面PBE所成二面角为锐角,
∴平面PAD和平面PBE所成二面角的余弦值为 ![]() .
.
【解析】(I)根据菱形的性质得出BE⊥AB,由PA⊥平面ABCD得出PA⊥BE,故而BE⊥平面PAB,于是结论得证;(II)设AC,BD交点为O,以O为原点建立坐标系,求出两个平面的法向量 ![]() ,则|cos<
,则|cos< ![]() >|即为所求.
>|即为所求.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案