题目内容
【题目】一个几何体的三视图如图所示（单位：m），求该几何体的体积和表面积．（V圆锥体= 
Sh，V圆柱体=Sh） 
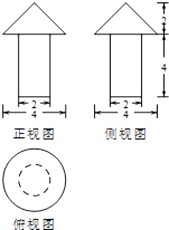
【答案】解：根据几何体的三视图，得； 该几何体是底面直径为2，高为4的圆柱，与底面直径为4，高为2的圆锥的组合体；
其中圆锥的母线为 
=2 
，
∴该几何体的体积为，
V=V柱+V锥=π124+ 
π222= 
π；
表面积为：S=S底面圆+S圆柱侧+S圆锥侧=π22+2π14+π22 =（12+4 ）π
【解析】根据三视图得出该几何体是圆柱与圆锥的组合体；求出它的体积与表面积即可．
【考点精析】解答此题的关键在于理解由三视图求面积、体积的相关知识，掌握求体积的关键是求出底面积和高；求全面积的关键是求出各个侧面的面积．
练习册系列答案
相关题目
