题目内容
12.随着人们低碳出行意识的提高,低碳节能小排量(小于或等于1.3L)汽车阅历越受私家购买者青睐,工信部为比较A,B两种小排量汽车的100km综合工况油耗,各随机选100辆汽车进行综合工况油耗检测,表1和表2分别是汽车A额B的综合工况检测的结果.表1:A种汽车综合工况油耗的频数分布表
| 100km综合工况油耗(L) | [5.2,5.4) | [5.4,5.6) | [5.6,5.8) | [5.8,6.0] |
| 频数 | 10 | 20 | 40 | 30 |
| 100km综合工况油耗(L) | [5.2,5.4) | [5.2,5.4) | [5.6,5.8) | [5.8,6.0) | [6.0,6.2] |
| 频数 | 15 | 30 | 20 | 25 | 10 |

(2)据此样本分析,估计1000辆A种汽车都行驶100km的综合工况油耗总量约为多少(单位:L)(同一组中的数据用该区间的中点值做代表).
(3)完成下面2×2列联表,并回答是否有95%的把握认为“A中汽车与B中汽车的100km综合工况油耗由差异”:

附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(b+d)}$,其中,n=a+b+c+d.
| P(K2≥k0) | 0.100 | 0.05 | 0.025 |
| k0 | 2.706 | 3.841 | 5.024 |
分析 (1)利用数据,完成下面频率分布直观图;
(2)求出每辆A种汽车都行驶100km的综合工况油耗量,即可估计1000辆A种汽车都行驶100km的综合工况油耗总量;
(3)利用数据,完成×2列联表,计算K2,即可回答是否有95%的把握认为“A中汽车与B中汽车的100km综合工况油耗由差异”.
解答 解:(1)由题意,可得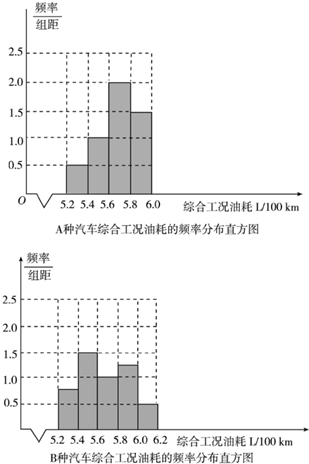
(2)每辆A种汽车都行驶100km的综合工况油耗量$\overline{x}$=5.3×0.1+5.5×0.2+5.7×0.4+5.9×0.3=5.68,
∴1000辆A种汽车都行驶100km的综合工况油耗总量约为5680L;
(3)
| 100km综合工况油耗不小于5.6L | 100km综合工况油耗油耗小于5.6L | 合计 | |
| A种汽车 | a=70 | b=30 | 100 |
| B种汽车 | c=55 | d=45 | 100 |
| 125 | 75 | n=200 |
∴有95%的把握认为“A中汽车与B中汽车的100km综合工况油耗由差异”.
点评 本题考查频率分布直观图,考查独立性检验,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
3.从平行六面体的8个顶点中任取5个顶点为顶点,恰好构成四棱锥的概率为( )
| A. | $\frac{1}{7}$ | B. | $\frac{2}{7}$ | C. | $\frac{3}{7}$ | D. | $\frac{6}{7}$ |
20.在△ABC中,角A,B,C所对的边分别为a,b,c,已知a=2$\sqrt{3}$,c=2$\sqrt{2}$,1+$\frac{tanA}{tanB}$=$\frac{2c}{b}$.则∠C=( )
| A. | 30° | B. | 135° | C. | 45°或135° | D. | 45° |
4.已知cosα=$\frac{4}{5}$,α∈(-$\frac{π}{2}$,0),则tan($\frac{π}{4}$+$\frac{α}{2}$)的值是( )
| A. | 2 | B. | $\frac{2}{5}$ | C. | -2 | D. | -$\frac{1}{2}$ |
2.若函数y=f(x)是函数y=($\frac{1}{2}$)x的反函数,则f(4)=( )
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |