题目内容
F1、F2是双曲线C:x2- 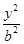 =1的两个焦点,P是C上一点,且△F1PF2是等腰直角三角形,则双曲线C的离心率为
=1的两个焦点,P是C上一点,且△F1PF2是等腰直角三角形,则双曲线C的离心率为
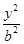 =1的两个焦点,P是C上一点,且△F1PF2是等腰直角三角形,则双曲线C的离心率为
=1的两个焦点,P是C上一点,且△F1PF2是等腰直角三角形,则双曲线C的离心率为A.1+ | B.2+ |
C.3- | D.3+ |
A
解:由△PF1F2为等腰直角三角形,又|PF1|≠|PF2|,
故必有|F1F2|=|PF2|,即2c= ,从而得c2-2ac-a2=0,即e2-2e-1=0,
,从而得c2-2ac-a2=0,即e2-2e-1=0,
解之得e=1±
∵e>1,∴e=1+
故选:A.
故必有|F1F2|=|PF2|,即2c=
 ,从而得c2-2ac-a2=0,即e2-2e-1=0,
,从而得c2-2ac-a2=0,即e2-2e-1=0,解之得e=1±

∵e>1,∴e=1+

故选:A.

练习册系列答案
相关题目
 为圆
为圆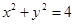 上的动点,且
上的动点,且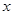 轴上,
轴上,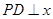 轴,垂足为
轴,垂足为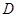 ,线段
,线段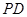 中点
中点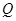 的轨迹为曲线
的轨迹为曲线 ,过定点
,过定点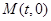
 任作一条与
任作一条与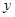 轴不垂直的直线
轴不垂直的直线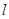 ,它与曲线
,它与曲线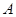 、
、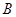 两点。
两点。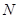 ,使得
,使得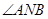 总能被
总能被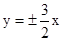 ,则其离心率是为 .
,则其离心率是为 . 与平面上两定点
与平面上两定点 、
、 连线的斜率的积为定
连线的斜率的积为定 .
. ;(2)设直线
;(2)设直线 与曲线
与曲线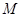 、
、 两点,当|
两点,当| |=
|= 时,求直线
时,求直线 的方程.
的方程. 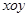 上取两个定点
上取两个定点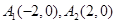 ,再取两个动点
,再取两个动点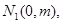
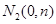 ,且
,且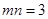 .
.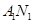 与
与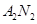 交点的轨迹
交点的轨迹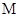 的方程;
的方程;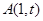 (
(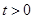 )是轨迹
)是轨迹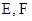 是轨迹
是轨迹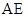 的斜率
的斜率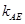 与直线
与直线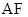 的斜率
的斜率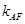 满足
满足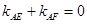 ,试探究直线
,试探究直线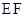 的斜率是否是定值?若是定值,求出这个定值,若不是,说明理由.
的斜率是否是定值?若是定值,求出这个定值,若不是,说明理由. 上的任意一点到它两个焦点
上的任意一点到它两个焦点 的距离之和为
的距离之和为 ,且它的焦距为2.
,且它的焦距为2. 的方程;
的方程; 与椭圆
与椭圆 ,且线段
,且线段 的中点
的中点 不在圆
不在圆 内,求实数
内,求实数 的取值范围.
的取值范围. ;
;
 轴的正半轴的交点,求四边形OADB的最大面积及D点坐标.
轴的正半轴的交点,求四边形OADB的最大面积及D点坐标. ,直线AM,BM相交于点M,且它们的斜率之和是2,则点M的轨迹方程是( )
,直线AM,BM相交于点M,且它们的斜率之和是2,则点M的轨迹方程是( )



 的左右焦点,过F1的直线与左支交于A、B两点,若
的左右焦点,过F1的直线与左支交于A、B两点,若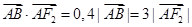 ,则该双曲线的离心率是为( )
,则该双曲线的离心率是为( ) B.
B. C.
C.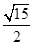 D.
D.