题目内容
已知圆C方程:(x-1)2 + y 2=9,垂直于x轴的直线L与圆C相切于N点(N在圆心C的右侧),平面上有一动点P,若PQ⊥L,垂足为Q,且 ;
;

(1)求点P的轨迹方程;
(2)已知D为点P的轨迹曲线上第一象限弧上一点,O为原点,A、B分别为点P的轨迹曲线与 轴的正半轴的交点,求四边形OADB的最大面积及D点坐标.
轴的正半轴的交点,求四边形OADB的最大面积及D点坐标.
 ;
;
(1)求点P的轨迹方程;
(2)已知D为点P的轨迹曲线上第一象限弧上一点,O为原点,A、B分别为点P的轨迹曲线与
 轴的正半轴的交点,求四边形OADB的最大面积及D点坐标.
轴的正半轴的交点,求四边形OADB的最大面积及D点坐标.(1)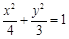 (2)四边形
(2)四边形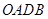 的最大面积为
的最大面积为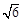 ,
,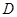 点坐标为
点坐标为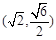
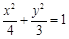 (2)四边形
(2)四边形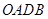 的最大面积为
的最大面积为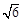 ,
,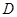 点坐标为
点坐标为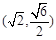
(1)设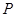 点坐标为
点坐标为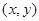 ,然后对其
,然后对其 坐标化,然后化简即可求得点P的轨迹方程.
坐标化,然后化简即可求得点P的轨迹方程.
(2)本小题为研究方便,可以设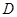 点坐标为
点坐标为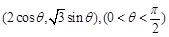
然后再四边形OADB的面积表示成关于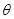 的三角函数求研究其最值.
的三角函数求研究其最值.
解:(1)设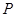 点坐标为
点坐标为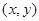 ,…………………1分
,…………………1分
则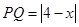 ,……………2分
,……………2分
 …………………………3分
…………………………3分
因为 ,所以
,所以 , …………………4分
, …………………4分
化简得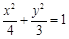 ………………………………5分
………………………………5分
所以点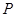 的轨迹方程是
的轨迹方程是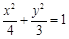 ………………6分
………………6分
(2)依题意得,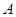 点坐标为
点坐标为 ,
,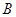 点坐标为
点坐标为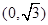 ……………7分
……………7分
设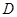 点坐标为
点坐标为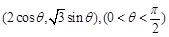 ,……………8分
,……………8分
则四边形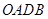 的面积
的面积 ,………………………9分
,………………………9分
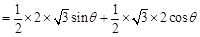 ………………10分
………………10分
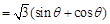
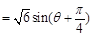 …………………11分
…………………11分
又因为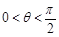 ,所以
,所以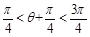 …………………………12分
…………………………12分
所以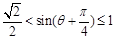 ,即
,即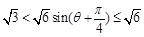
所以四边形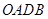 的最大面积为
的最大面积为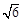 ,………………………………………13分
,………………………………………13分
当四边形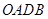 的面积取最大时,
的面积取最大时,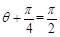 ,即
,即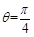 ,
,
此时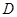 点坐标为
点坐标为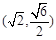 ………………………………………………………………14分
………………………………………………………………14分
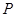 点坐标为
点坐标为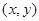 ,然后对其
,然后对其 坐标化,然后化简即可求得点P的轨迹方程.
坐标化,然后化简即可求得点P的轨迹方程.(2)本小题为研究方便,可以设
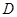 点坐标为
点坐标为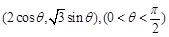
然后再四边形OADB的面积表示成关于
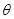 的三角函数求研究其最值.
的三角函数求研究其最值.解:(1)设
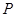 点坐标为
点坐标为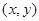 ,…………………1分
,…………………1分则
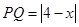 ,……………2分
,……………2分 …………………………3分
…………………………3分因为
 ,所以
,所以 , …………………4分
, …………………4分化简得
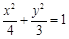 ………………………………5分
………………………………5分所以点
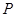 的轨迹方程是
的轨迹方程是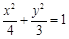 ………………6分
………………6分(2)依题意得,
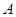 点坐标为
点坐标为 ,
,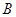 点坐标为
点坐标为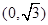 ……………7分
……………7分设
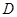 点坐标为
点坐标为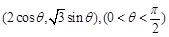 ,……………8分
,……………8分则四边形
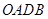 的面积
的面积 ,………………………9分
,………………………9分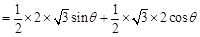 ………………10分
………………10分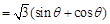
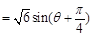 …………………11分
…………………11分又因为
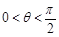 ,所以
,所以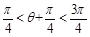 …………………………12分
…………………………12分所以
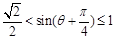 ,即
,即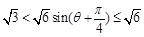
所以四边形
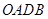 的最大面积为
的最大面积为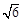 ,………………………………………13分
,………………………………………13分当四边形
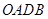 的面积取最大时,
的面积取最大时,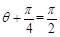 ,即
,即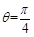 ,
,此时
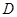 点坐标为
点坐标为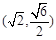 ………………………………………………………………14分
………………………………………………………………14分
练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目

 中,椭圆
中,椭圆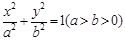 的左、右焦点分别为
的左、右焦点分别为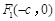 ,
,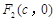 .已知
.已知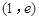 和
和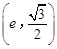 都在椭圆上,其中
都在椭圆上,其中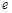 为椭圆的离心率.
为椭圆的离心率.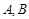 是椭圆上位于
是椭圆上位于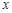 轴上方的两点,且直线
轴上方的两点,且直线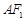 与直线
与直线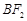 平行,
平行,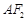 与
与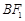 交于点P.
交于点P.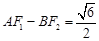 ,求直线
,求直线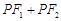 是定值.
是定值.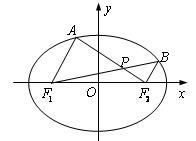
 和F分别为椭圆
和F分别为椭圆
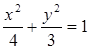 的中心和左焦点,点P为椭圆上的任意点,则
的中心和左焦点,点P为椭圆上的任意点,则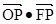 的最大值是( )
的最大值是( ) 是曲线
是曲线 上任意一点,则点
上任意一点,则点 的最小距离是( )
的最小距离是( ) 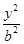 =1的两个焦点,P是C上一点,且△F1PF2是等腰直角三角形,则双曲线C的离心率为
=1的两个焦点,P是C上一点,且△F1PF2是等腰直角三角形,则双曲线C的离心率为
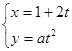 ,(t为参数,a∈R)点M(5,4)在该曲线上,(1)求常数a;(2)求曲线C的普通方程。
,(t为参数,a∈R)点M(5,4)在该曲线上,(1)求常数a;(2)求曲线C的普通方程。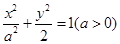 的左、右焦点分别为F1、F2,A是椭圆C上的一点,
的左、右焦点分别为F1、F2,A是椭圆C上的一点,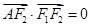 ,坐标原点O到直线AF1的距离为
,坐标原点O到直线AF1的距离为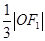 .
.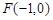 ,交 y 轴于点M,若
,交 y 轴于点M,若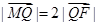 ,求直线l 的斜率.
,求直线l 的斜率.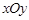 中,若双曲线
中,若双曲线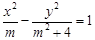 的离心率为
的离心率为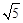 ,则
,则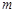 的值为 .
的值为 .