题目内容
在直角坐标系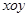 上取两个定点
上取两个定点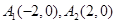 ,再取两个动点
,再取两个动点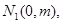
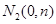 ,且
,且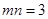 .
.
(Ⅰ)求直线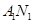 与
与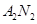 交点的轨迹
交点的轨迹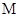 的方程;
的方程;
(Ⅱ)已知点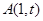 (
(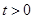 )是轨迹
)是轨迹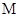 上的定点,
上的定点,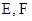 是轨迹
是轨迹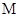 上的两个动点,如果直线
上的两个动点,如果直线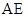 的斜率
的斜率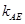 与直线
与直线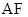 的斜率
的斜率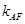 满足
满足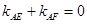 ,试探究直线
,试探究直线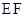 的斜率是否是定值?若是定值,求出这个定值,若不是,说明理由.
的斜率是否是定值?若是定值,求出这个定值,若不是,说明理由.
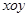 上取两个定点
上取两个定点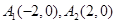 ,再取两个动点
,再取两个动点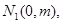
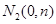 ,且
,且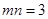 .
.(Ⅰ)求直线
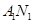 与
与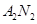 交点的轨迹
交点的轨迹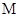 的方程;
的方程;(Ⅱ)已知点
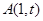 (
(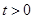 )是轨迹
)是轨迹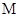 上的定点,
上的定点,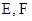 是轨迹
是轨迹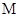 上的两个动点,如果直线
上的两个动点,如果直线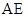 的斜率
的斜率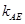 与直线
与直线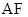 的斜率
的斜率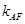 满足
满足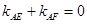 ,试探究直线
,试探究直线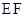 的斜率是否是定值?若是定值,求出这个定值,若不是,说明理由.
的斜率是否是定值?若是定值,求出这个定值,若不是,说明理由.解:(Ⅰ)轨迹M的方程为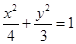 (
(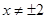 )
)
(Ⅱ)直线EF的斜率为定值,其值为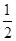
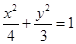 (
(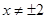 )
)(Ⅱ)直线EF的斜率为定值,其值为
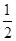
本试题主要考查了直线与直线的位置关系,以及直线与椭圆的位置关系的综合运用。(1) 依题意知直线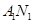 的方程为:
的方程为: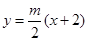 ,直线
,直线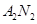 的方程为:
的方程为: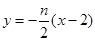 ,利用交轨法得到轨迹方程的求解。
,利用交轨法得到轨迹方程的求解。
(2)设出直线方程与椭圆方程联立,运用韦达定理,和斜率公示得到结论。
(Ⅰ)依题意知直线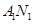 的方程为:
的方程为: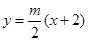 ①……………2分
①……………2分
直线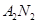 的方程为:
的方程为: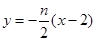 ②…………………3分
②…………………3分
设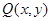 是直线
是直线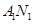 与
与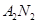 交点,①×②得
交点,①×②得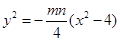
由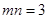 整理得
整理得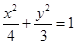 …………………4分
…………………4分
∵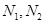 不与原点重合 ∴点
不与原点重合 ∴点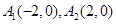 不在轨迹M上…………………5分
不在轨迹M上…………………5分
∴轨迹M的方程为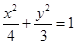 (
(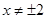 )…………………6分
)…………………6分
(Ⅱ)∵点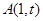 (
(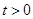 )在轨迹M上 ∴
)在轨迹M上 ∴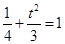 解得
解得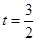 ,即点A的坐标为
,即点A的坐标为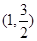
设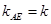 ,则直线AE方程为:
,则直线AE方程为: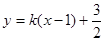 ,代入
,代入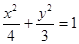 并整理得
并整理得
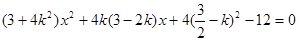 …………………9分
…………………9分
设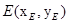 ,
,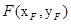 , ∵点
, ∵点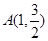 在轨迹M上,
在轨迹M上,
∴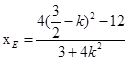 ③,
③, 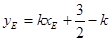 ④………………11分
④………………11分
又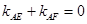 得
得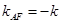 ,将③、④式中的
,将③、④式中的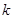 代换成
代换成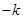 ,可得
,可得
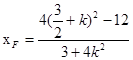 ,
,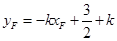 …………………………12分
…………………………12分
∴直线EF的斜率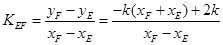 …………………13分
…………………13分
∵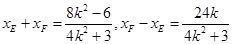
∴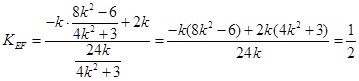
即直线EF的斜率为定值,其值为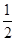
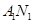 的方程为:
的方程为: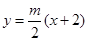 ,直线
,直线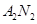 的方程为:
的方程为: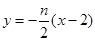 ,利用交轨法得到轨迹方程的求解。
,利用交轨法得到轨迹方程的求解。(2)设出直线方程与椭圆方程联立,运用韦达定理,和斜率公示得到结论。
(Ⅰ)依题意知直线
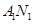 的方程为:
的方程为: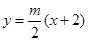 ①……………2分
①……………2分直线
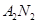 的方程为:
的方程为: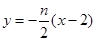 ②…………………3分
②…………………3分设
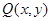 是直线
是直线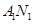 与
与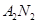 交点,①×②得
交点,①×②得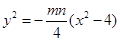
由
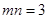 整理得
整理得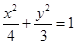 …………………4分
…………………4分∵
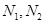 不与原点重合 ∴点
不与原点重合 ∴点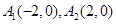 不在轨迹M上…………………5分
不在轨迹M上…………………5分∴轨迹M的方程为
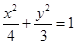 (
(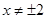 )…………………6分
)…………………6分(Ⅱ)∵点
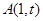 (
(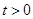 )在轨迹M上 ∴
)在轨迹M上 ∴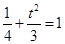 解得
解得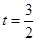 ,即点A的坐标为
,即点A的坐标为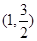
设
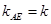 ,则直线AE方程为:
,则直线AE方程为: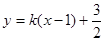 ,代入
,代入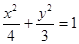 并整理得
并整理得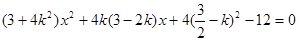 …………………9分
…………………9分设
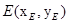 ,
,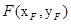 , ∵点
, ∵点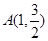 在轨迹M上,
在轨迹M上,∴
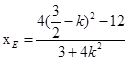 ③,
③, 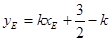 ④………………11分
④………………11分又
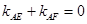 得
得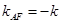 ,将③、④式中的
,将③、④式中的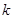 代换成
代换成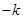 ,可得
,可得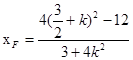 ,
,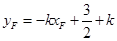 …………………………12分
…………………………12分∴直线EF的斜率
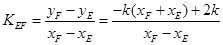 …………………13分
…………………13分∵
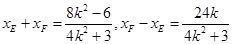
∴
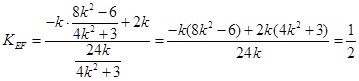
即直线EF的斜率为定值,其值为
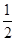

练习册系列答案
相关题目
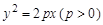 的焦点与椭圆
的焦点与椭圆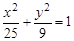 的一个焦点重合,过点
的一个焦点重合,过点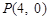 的直线与抛物线交于
的直线与抛物线交于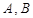 两点,若
两点,若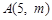 ,则
,则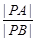 的值( )
的值( )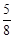
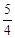
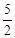
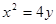 的焦点F作直线交抛物线于
的焦点F作直线交抛物线于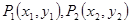 两点,若
两点,若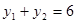 ,则
,则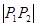 的值为( )
的值为( )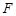 为抛物线
为抛物线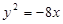 的焦点,
的焦点,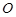 为原点,点
为原点,点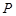 是抛物线准线上一动点,点
是抛物线准线上一动点,点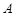 在抛物线上,且
在抛物线上,且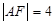 ,则
,则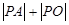 的最小值为 ( )
的最小值为 ( )


 是曲线
是曲线 上任意一点,则点
上任意一点,则点 的最小距离是( )
的最小距离是( ) 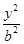 =1的两个焦点,P是C上一点,且△F1PF2是等腰直角三角形,则双曲线C的离心率为
=1的两个焦点,P是C上一点,且△F1PF2是等腰直角三角形,则双曲线C的离心率为
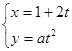 ,(t为参数,a∈R)点M(5,4)在该曲线上,(1)求常数a;(2)求曲线C的普通方程。
,(t为参数,a∈R)点M(5,4)在该曲线上,(1)求常数a;(2)求曲线C的普通方程。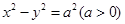 的左、右顶点分别为
的左、右顶点分别为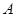 、
、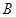 ,点
,点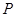 是第一象限内双曲线上的点.若直线
是第一象限内双曲线上的点.若直线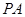 、
、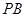 的倾斜角分别为
的倾斜角分别为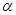 ,
,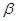 ,且
,且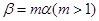 ,那么
,那么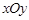 中,若双曲线
中,若双曲线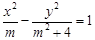 的离心率为
的离心率为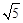 ,则
,则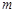 的值为 .
的值为 .