题目内容
11.函数f(x)=sin(x+10°)+sin(x+70°)的最大值是( )| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
分析 把sin(x+70°)转化为sin(x+10°+60°)利用两次两角和公式化简,利用正弦函数的性质求得最小值.
解答 解:f(x)=sin(x+10°)+sin(x+70°)
=sin(x+10°)+sin(x+10°+60°)
=sin(x+10°)+$\frac{1}{2}$sin(x+10°)+$\frac{\sqrt{3}}{2}$cos(x+10°)
=$\frac{3}{2}$sin(x+10°)+$\frac{\sqrt{3}}{2}$cos(x+10°)
=$\sqrt{3}$sin(x+10°+30°)
=$\sqrt{3}$sin(x+40°),
∴当sin(x+40°)=1时,函数有最大值.
点评 本题主要考查了两角和公式的运用,三角函数的图象与性质.考查了学生对三角函数公式熟练记忆.

练习册系列答案
相关题目
1.一只小狗在如图所示的方砖上走来走去,求最终停在阴影方砖上的概率为( )
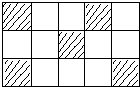

| A. | $\frac{3}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{3}$ | D. | $\frac{5}{12}$ |
6.已知F1、F2为椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{169}$=1的两个焦点,过F1的直线交椭圆于A、B两点.若|F2A|+|F2B|=30,则|AB|=( )
| A. | 16 | B. | 18 | C. | 22 | D. | 20 |
3.执行如图的程序框图,若输出的k=2,则输入x的取值范围是( )
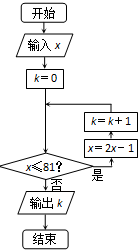

| A. | (21,41) | B. | [21,41] | C. | (21,41] | D. | [21,41) |