��Ŀ����
13�������ĸ������У��ٴ����ٴ��ݵIJ�Ʒ������ˮ���ϣ��ʼ�Աÿ10���Ӵ��г�ȡһ����Ʒ����ij��ָ���⣬�����ij����Ƿֲ������
�ڶ�������p��?x��R��ʹ��x2+x+1��0����Vp��?x��R������x2+x+1��0��
�ۡ�x��1��y��2���ǡ�x+y��3���ı�Ҫ�����������
������������������������Խǿ�������ϵ����Խ�ӽ���1��
����������ĸ���Ϊ��������
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
���� �ɳ����������֪ʶ�Լ����ϵ�����ѡ���жϼ��ɣ�
��� �⣺�ٴ����ٴ��ݵIJ�Ʒ������ˮ���ϣ��ʼ�Աÿ10���Ӵ��г�ȡһ����Ʒ����ij��ָ���⣬
�����ij������Ƿֲ����������ϵͳ�������ʴ���
�ڶ�������p��?x��R��ʹ��x2+x+1��0����Vp��?x��R������x2+x+1��0��
���س�����ķ��ɿ�֪��ȷ��
�ۡ�x��1��y��2�������Ƴ���x+y��3������x+y��3�����Ƴ���x��1��y��2����
��Ӧ�DZ�Ҫ�������������ȷ��
������������������������Խǿ�������ϵ���ľ���ֵ��Խ�ӽ���1���ʴ���
��ѡ��B
���� ���⿼��������ٵ��ж����漰�����������֪ʶ�Լ����ϵ�������е��⣮

��ϰ��ϵ�д�
�����Ŀ
11������f��x��=sin��x+10�㣩+sin��x+70�㣩�����ֵ�ǣ�������
| A�� | 1 | B�� | 2 | C�� | $\sqrt{2}$ | D�� | $\sqrt{3}$ |
1����֪a��0��������ʽloga+3x-loga+1x+5��n+$\frac{6}{n}$������n��N*���������ʵ��x��ȡֵ��Χ�ǣ�������
| A�� | [1��+�ޣ� | B�� | ��0��1] | C�� | [3��+�ޣ� | D�� | [1��3] |
2��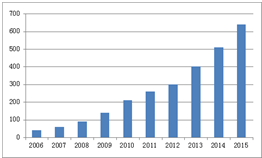 ij��ӰԺͳ�Ƶ�Ӱ��ӳ���ε������ͼ��ʾ�����к���ģ���У�����ʽ���������Ӱ��ӳ��������仯���ɵ��ǣ�������
ij��ӰԺͳ�Ƶ�Ӱ��ӳ���ε������ͼ��ʾ�����к���ģ���У�����ʽ���������Ӱ��ӳ��������仯���ɵ��ǣ�������
 ij��ӰԺͳ�Ƶ�Ӱ��ӳ���ε������ͼ��ʾ�����к���ģ���У�����ʽ���������Ӱ��ӳ��������仯���ɵ��ǣ�������
ij��ӰԺͳ�Ƶ�Ӱ��ӳ���ε������ͼ��ʾ�����к���ģ���У�����ʽ���������Ӱ��ӳ��������仯���ɵ��ǣ�������| A�� | y=ax2+bx+c | B�� | y=aex+b | C�� | y=ax3+b | D�� | y=alnx+b |