题目内容
12.椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{3}}{2}$,长轴端点A与短轴端点B间的距离为$\sqrt{5}$.(Ⅰ)求椭圆C的方程;
(Ⅱ)P为椭圆C上一动点,求△PAB的面积的最大值.
分析 (Ⅰ)通过$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,$\sqrt{{a}^{2}+{b}^{2}}$,利用a2=b2+c2,计算即得结论;
(Ⅱ)只需求出位于直线AB下方且与椭圆相切的直线l的方程,利用两点间距离公式、三角形面积公式计算即可.
解答 解:(Ⅰ)由已知e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,$\sqrt{{a}^{2}+{b}^{2}}$=$\sqrt{5}$,
又a2=b2+c2,解得a2=4,b2=1,
∴椭圆C的方程为:$\frac{{x}^{2}}{4}+{y}^{2}=1$;
(Ⅱ)∵kAB=$\frac{1-0}{0-2}$=-$\frac{1}{2}$,直线AB方程为:y=-$\frac{1}{2}$x+1,
∴可设与AB平行的直线l为:y=-$\frac{1}{2}$x+b,
联立$\left\{\begin{array}{l}{y=-\frac{1}{2}x+b}\\{\frac{{x}^{2}}{4}+{y}^{2}=1}\end{array}\right.$,消去y整理得:x2-2bx+2b2-2=0,
令△=(-2b)2-4(2b2-2)=0,解得:b=±$\sqrt{2}$,
显然当b=-$\sqrt{2}$时,直线l与椭圆的交点P与A、B组成的三角形的面积最大,
由已知|AB|=$\sqrt{5}$,
△PAB中AB边上的高d=$\frac{2\sqrt{2}+2}{\sqrt{1+{2}^{2}}}$=$\frac{2\sqrt{2}+2}{\sqrt{5}}$,
∴S△PAB=$\frac{1}{2}$|AB|•d=$\frac{1}{2}$•$\sqrt{5}$•$\frac{2\sqrt{2}+2}{\sqrt{5}}$=$\sqrt{2}+1$.
点评 本题是一道直线与圆锥曲线的综合题,考查运算求解能力,考查分析问题、解决问题的能力,注意解题方法的积累,属于中档题.

| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
| A. | [1,+∞) | B. | (0,1] | C. | [3,+∞) | D. | [1,3] |
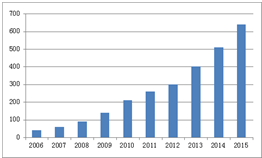 某电影院统计电影放映场次的情况如图所示.下列函数模型中,最不合适近似描述电影放映场次逐年变化规律的是( )
某电影院统计电影放映场次的情况如图所示.下列函数模型中,最不合适近似描述电影放映场次逐年变化规律的是( )| A. | y=ax2+bx+c | B. | y=aex+b | C. | y=ax3+b | D. | y=alnx+b |
 如图所示,圆锥顶点为P,底面圆心为O,AB和CD是底面圆O上的两条平行弦,证明:平面PAD与平面PCD的交线平行于底面.
如图所示,圆锥顶点为P,底面圆心为O,AB和CD是底面圆O上的两条平行弦,证明:平面PAD与平面PCD的交线平行于底面.