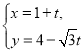题目内容
【题目】已知函数f(x)![]() x2+ax+lnx(a∈R)
x2+ax+lnx(a∈R)
(1)讨论函数f(x)的单调性;
(2)若f(x)存在两个极值点x1,x2且|x1﹣x2|![]() ,求|f(x1)﹣f(x2)|的最大值.
,求|f(x1)﹣f(x2)|的最大值.
【答案】(1)答案不唯一,具体见解析(2)![]()
【解析】
(1)求导可得![]() ,再分
,再分![]() ,
,![]() 讨论
讨论![]() 与0的大小关系,进而得出单调性情况;
与0的大小关系,进而得出单调性情况;
(2)表示出![]() ,构造函数
,构造函数![]() ,利用导数求其最大值即可.
,利用导数求其最大值即可.
(1)![]() ,设μ(x)=x2+ax+1,则μ(0)=1>0,对称轴为
,设μ(x)=x2+ax+1,则μ(0)=1>0,对称轴为![]() ,
,
①当![]() ,即a≥0时,在(0,+∞)上,
,即a≥0时,在(0,+∞)上,![]() >0,f(x)是增函数;
>0,f(x)是增函数;
②当![]() ,即a<0时,
,即a<0时,![]() =a2﹣4=0得a=±2,
=a2﹣4=0得a=±2,
(i)当﹣2≤a<0时,在(0,+∞)上,![]() >0,f(x)是增函数;
>0,f(x)是增函数;
(ii)当a<﹣2时,令![]() =0得
=0得![]() ,
,
在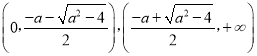 上,
上,![]() >0,f(x)是增函数;
>0,f(x)是增函数;
在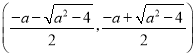 上,
上,![]() <0,f(x)是减函数;
<0,f(x)是减函数;
(2)由(1)知,f(x)得两个极值点x1,x2满足x2+ax+1=0,故x1+x2=﹣a,x1x2=1,
不妨设0<x1<1<x2,则f(x)在(x1,x2)上是减函数,
∴![]() ,
,
令![]() ,设函数
,设函数![]() ,则
,则![]() ,
,
∴h(t)在(1,+∞)上为增函数,
由![]() ,则
,则![]() ,解得1<x2≤2,故
,解得1<x2≤2,故![]() ,
,
∴![]() ,
,
∴|f(x1)﹣f(x2)|的最大值为![]() .
.

 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
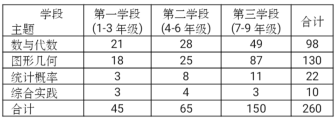
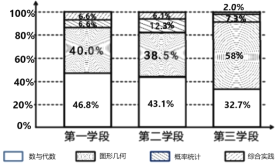
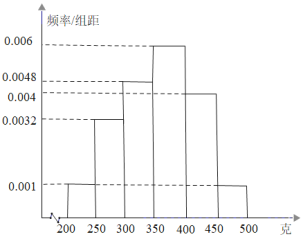
小学期末标准试卷系列答案【题目】为了解某初中学校学生睡眠状况,在该校全体学生中随机抽取了容量为120的样本,统计睡眠时间(单位:![]() ).经统计,时间均在区间
).经统计,时间均在区间![]() 内,将其按
内,将其按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成6组,制成如图所示的频率分布直方图:
分成6组,制成如图所示的频率分布直方图:

(1)世界卫生组织表明,该年龄段的学生睡眠时间![]() 服从正态分布
服从正态分布![]() ,其标准为:该年龄段的学生睡眠时间的平均值
,其标准为:该年龄段的学生睡眠时间的平均值![]() ,方差
,方差![]() .根据
.根据![]() 原则,用样本估计总体,判断该初中学校学生睡眠时间在区间
原则,用样本估计总体,判断该初中学校学生睡眠时间在区间![]() 上是否达标?
上是否达标?
(参考公式:![]() ,
,![]() ,
,![]() )
)
(2)若规定睡眠时间不低于![]() 为优质睡眠.已知所抽取的这120名学生中,男、女睡眠质量人数如下
为优质睡眠.已知所抽取的这120名学生中,男、女睡眠质量人数如下![]() 列联表所示:
列联表所示:
优质睡眠 | 非优质睡眠 | 合计 | |
男 | 60 | ||
女 | 19 | ||
合计 |
将列联表数据补充完整,并判断是否有![]() 的把握认为优质睡眠与性别有关系,并说明理由;
的把握认为优质睡眠与性别有关系,并说明理由;
下面的临界值表仅供参考:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: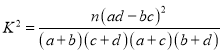 ,其中
,其中![]() .)
.)