ĖâÄŋÄÚČÝ
ĄūĖâÄŋĄŋΊÁË―âÄģģõÖÐŅ§ÐĢŅ§ÉúËŊÃßŨīŋöĢŽÔÚļÃÐĢČŦĖåŅ§ÉúÖÐËæŧúģéČĄÁËČÝÁŋΊ120ĩÄŅųąūĢŽÍģžÆËŊÃßĘąžäĢĻĩĨÎŧĢš![]() ĢĐ.ūÍģžÆĢŽĘąžäūųÔÚĮøžä
ĢĐ.ūÍģžÆĢŽĘąžäūųÔÚĮøžä![]() ÄÚĢŽ―ŦÆä°ī
ÄÚĢŽ―ŦÆä°ī![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ![]() ·ÖģÉ6ŨéĢŽÖÆģÉČįÍžËųĘūĩÄÆĩÂĘ·ÖēžÖą·―ÍžĢš
·ÖģÉ6ŨéĢŽÖÆģÉČįÍžËųĘūĩÄÆĩÂĘ·ÖēžÖą·―ÍžĢš

ĢĻ1ĢĐĘĀ―įÎĀÉúŨéÖŊąíÃũĢŽļÃÄęÁäķÎĩÄŅ§ÉúËŊÃßĘąžä![]() ·þīÓÕýĖŽ·Öēž
·þīÓÕýĖŽ·Öēž![]() ĢŽÆäąęŨžÎŠĢšļÃÄęÁäķÎĩÄŅ§ÉúËŊÃßĘąžäĩÄÆ―ūųÖĩ
ĢŽÆäąęŨžÎŠĢšļÃÄęÁäķÎĩÄŅ§ÉúËŊÃßĘąžäĩÄÆ―ūųÖĩ![]() ĢŽ·―ēî
ĢŽ·―ēî![]() .ļųūÝ
.ļųūÝ![]() ÔÔōĢŽÓÃŅųąūđĀžÆŨÜĖåĢŽÅÐķÏļÃģõÖÐŅ§ÐĢŅ§ÉúËŊÃßĘąžäÔÚĮøžä
ÔÔōĢŽÓÃŅųąūđĀžÆŨÜĖåĢŽÅÐķÏļÃģõÖÐŅ§ÐĢŅ§ÉúËŊÃßĘąžäÔÚĮøžä![]() ÉÏĘĮ·ņīïąęĢŋ
ÉÏĘĮ·ņīïąęĢŋ
ĢĻēÎŋžđŦĘ―Ģš![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ![]() ĢĐ
ĢĐ
ĢĻ2ĢĐČôđæķĻËŊÃßĘąžäēŧĩÍÓÚ![]() ΊÓÅÖĘËŊÃß.ŌŅÖŠËųģéČĄĩÄÕâ120ÃûŅ§ÉúÖÐĢŽÄÐĄĒÅŪËŊÃßÖĘÁŋČËĘýČįÏÂ
ΊÓÅÖĘËŊÃß.ŌŅÖŠËųģéČĄĩÄÕâ120ÃûŅ§ÉúÖÐĢŽÄÐĄĒÅŪËŊÃßÖĘÁŋČËĘýČįÏÂ![]() ÁÐÁŠąíËųĘūĢš
ÁÐÁŠąíËųĘūĢš
ÓÅÖĘËŊÃß | ·ĮÓÅÖĘËŊÃß | šÏžÆ | |
ÄÐ | 60 | ||
ÅŪ | 19 | ||
šÏžÆ |
―ŦÁÐÁŠąíĘýūÝēđģäÍęÕûĢŽēĒÅÐķÏĘĮ·ņÓÐ![]() ĩÄ°ŅÎÕČÏΊÓÅÖĘËŊÃßÓëÐÔąðÓÐđØÏĩĢŽēĒËĩÃũĀíÓÉĢŧ
ĩÄ°ŅÎÕČÏΊÓÅÖĘËŊÃßÓëÐÔąðÓÐđØÏĩĢŽēĒËĩÃũĀíÓÉĢŧ
ÏÂÃæĩÄÁŲ―įÖĩąí―öđĐēÎŋžĢš
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
ĢĻēÎŋžđŦĘ―Ģš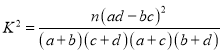 ĢŽÆäÖÐ
ĢŽÆäÖÐ![]() .ĢĐ
.ĢĐ
Ąūīð°ļĄŋĢĻ1ĢĐļÃÐĢŅ§ÉúËŊÃßĘąžäÔÚĮøžä![]() ÉÏēŧīïąęĢŧĢĻ2ĢĐÁÐÁŠąížû―âÎöĢŽÓÐ
ÉÏēŧīïąęĢŧĢĻ2ĢĐÁÐÁŠąížû―âÎöĢŽÓÐ![]() ĩÄ°ŅÎÕČÏΊÓÅÖĘËŊÃßÓëÐÔąðÓÐđØÏĩĢŧĀíÓÉžû―âÎö
ĩÄ°ŅÎÕČÏΊÓÅÖĘËŊÃßÓëÐÔąðÓÐđØÏĩĢŧĀíÓÉžû―âÎö
Ąū―âÎöĄŋ
ĢĻ1ĢĐļųūÝÆĩÂĘ·ÖēžÖą·―ÍžĮóģö![]() ĢŽĮóģö
ĢŽĮóģö![]() .ļųūÝÆĩÂĘ·ÖēžÖą·―ÍžĮóģöŅ§ÉúËŊÃßĘąžäÔÚĮøžä
.ļųūÝÆĩÂĘ·ÖēžÖą·―ÍžĮóģöŅ§ÉúËŊÃßĘąžäÔÚĮøžä![]() ÉÏĩÄļÅÂĘĢŽÓë
ÉÏĩÄļÅÂĘĢŽÓë![]() ąČ―ÏīóÐĄĢŽžīĩÃīð°ļĢŧ
ąČ―ÏīóÐĄĢŽžīĩÃīð°ļĢŧ
ĢĻ2ĢĐĮóģöŅųąūÖÐÓÅÖĘËŊÃßŅ§ÉúĩÄČËĘýĢŽēđČŦÁÐÁŠąíĢŽžÆËã![]() ĢŽļųūÝÁŲ―įÖĩąíŋÉĩÃ―áÂÛ.
ĢŽļųūÝÁŲ―įÖĩąíŋÉĩÃ―áÂÛ.
ĢĻ1ĢĐļųūÝÖą·―ÍžĘýūÝĢŽÓÐ![]() ĢŽ
ĢŽ
―âĩÃ![]() .
.
ÓÉÆ―ūųÖĩ![]() ĢŽŅųąū·―ēî
ĢŽŅųąū·―ēî![]() ĢŽĩÃ
ĢŽĩÃ![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ
Ôō![]() žīĮóŅųąūĘýūÝÖÐĮøžä
žīĮóŅųąūĘýūÝÖÐĮøžä![]() ÄÚĩÄļÅÂĘÖĩĢŽ
ÄÚĩÄļÅÂĘÖĩĢŽ
Ôō![]() ĢŽ
ĢŽ
ļÃÐĢŅ§ÉúËŊÃßĘąžäÔÚĮøžä![]() ÉÏēŧīïąę.
ÉÏēŧīïąę.
ĢĻ2ĢĐļųūÝÖą·―ÍžŋÉÖŠĢŽŅųąūÖÐÓÅÖĘËŊÃßŅ§ÉúÓÐ![]() ĢŽÁÐÁŠąíČįÏÂĢš
ĢŽÁÐÁŠąíČįÏÂĢš
ÓÅÖĘËŊÃß | ·ĮÓÅÖĘËŊÃß | šÏžÆ | |
ÄÐ | 11 | 60 | 71 |
ÅŪ | 19 | 30 | 49 |
šÏžÆ | 30 | 90 | 120 |
ŋÉĩÃ![]() ĢŽ
ĢŽ
ËųŌÔĢŽÓÐ![]() ĩÄ°ŅÎÕČÏΊÓÅÖĘËŊÃßÓëÐÔąðÓÐđØÏĩ.
ĩÄ°ŅÎÕČÏΊÓÅÖĘËŊÃßÓëÐÔąðÓÐđØÏĩ.

 ŨÖīĘūäÆŠÓëÍŽē―ŨũÎÄīïąęÏĩÁÐīð°ļ
ŨÖīĘūäÆŠÓëÍŽē―ŨũÎÄīïąęÏĩÁÐīð°ļĄūĖâÄŋĄŋÄģÐĢīÓ2011Äęĩ―2018ÄęēΞӥ°ąąÔžĄąĄ°ŧŠÔžĄąŋžĘÔķøŧņĩÞӷÖĩÄŅ§ÉúĢĻÃŋÎŧŅ§ÉúÖŧÄÜēΞӥ°ąąÔžĄąĄ°ŧŠÔžĄąÖÐĩÄŌŧÖÖŋžĘÔĢĐČËĘýŋÉŌÔÍĻđýŌÔÏÂąíļņ·īÓģģöĀī.ĢĻΊÁË·―ąãžÆËãĢŽ―Ŧ2011ÄęąāšÅΊ1ĢŽ2012ÄęąāšÅΊ2ĢŽŌĀīËĀāÍÆĢĐ
Äę·Ý | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
ČËĘý | 2 | 3 | 4 | 4 | 7 | 7 | 6 | 6 |
ĢĻ1ĢĐĮóÕâ°ËÄęĀīĢŽļÃÐĢēΞӥ°ąąÔžĄąĄ°ŧŠÔžĄąŋžĘÔķøŧņĩÞӷÖĩÄŅ§ÉúČËĘýĩÄÖÐÎŧĘýšÍ·―ēîĢŧ
ĢĻ2ĢĐļųūÝŨî―üÎåÄęĩÄĘýūÝĢŽĀûÓÃŨîÐĄķþģË·ĻĮóģö![]() Óë
Óë![]() ÖŪžäĩÄÏßÐÔŧØđé·―ģĖĢŽēĒŌĀīËÔĪēâļÃÐĢ2019ÄęēΞӥ°ąąÔžĄąĄ°ŧŠÔžĄąŋžĘÔķøŧņĩÞӷÖĩÄŅ§ÉúČËĘý.ĢĻ―áđûŌŠĮóËÄÉáÎåČëÖÁļöÎŧĢĐ
ÖŪžäĩÄÏßÐÔŧØđé·―ģĖĢŽēĒŌĀīËÔĪēâļÃÐĢ2019ÄęēΞӥ°ąąÔžĄąĄ°ŧŠÔžĄąŋžĘÔķøŧņĩÞӷÖĩÄŅ§ÉúČËĘý.ĢĻ―áđûŌŠĮóËÄÉáÎåČëÖÁļöÎŧĢĐ
ēÎŋžđŦĘ―Ģš .
.
ĄūĖâÄŋĄŋÄģÁũÐÐēĄąŽ·ĒÆÚžäĢŽÄģĘÐÎĀÉú·ĀŌßēŋÃÅļøģöĩÄÖÎÁÆ·―°ļÖÐÍÆžöÁËČýÖÖÖÎÁÆŌĐÎï![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ![]() ĢĻ
ĢĻ![]() ĢŽ
ĢŽ![]() ĢŽ
ĢŽ![]() ĩÄĘđÓÃĘĮŧĨģâĮŌÍęąļĩÄĢĐĢŽēĒĮŌļÐČūŧžÕß°īđæķĻķžĩÃĩ―ÁËŌĐÎïÖÎÁÆ.ŧžÕßÔÚđØÓÚÕâČýÖÖŌĐÎïĩÄÓÐđØēÎĘýž°ĘÐģĄĩũēéĘýūÝČįÏÂąíËųĘūĢšĢĻąíÖÐĩÄĘýūÝķžŌÔŌŧļöÁÆģĖžÆĢĐ
ĩÄĘđÓÃĘĮŧĨģâĮŌÍęąļĩÄĢĐĢŽēĒĮŌļÐČūŧžÕß°īđæķĻķžĩÃĩ―ÁËŌĐÎïÖÎÁÆ.ŧžÕßÔÚđØÓÚÕâČýÖÖŌĐÎïĩÄÓÐđØēÎĘýž°ĘÐģĄĩũēéĘýūÝČįÏÂąíËųĘūĢšĢĻąíÖÐĩÄĘýūÝķžŌÔŌŧļöÁÆģĖžÆĢĐ
|
|
|
|
ĩĨžÛĢĻĩĨÎŧĢšÔŠĢĐ | 600 | 1000 | 800 |
ÖÎÓúÂĘ |
|
|
|
ĘÐģĄĘđÓÃÁŋĢĻĩĨÎŧĢšČËĢĐ | 305 | 122 | 183 |
ĢĻĒņĢĐīÓļÐČūŧžÕßÖÐČÎČĄŌŧČËĢŽĘÔĮóÆäŌŧļöÁÆģĖąŧÖÎÓúĩÄļÅÂĘīóÔžĘĮķāÉŲĢŋ
ĢĻĒōĢĐĘÔđĀËãÃŋÃûļÐČūŧžÕßÔÚŌŧļöÁÆģĖĩÄŌĐÎïÖÎÁÆ·ŅÓÃÆ―ūųĘĮķāÉŲ.