题目内容
5．
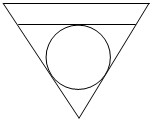如图，有一横截面为正三角形的圆锥形容器，内部盛水的高度为h，放入一个球后，水面恰好与球相切，求球的半径．
分析 根据题意，画出图形，结合图形利用正三角形的性质求出内切球的半径．
解答 解：如图所示，
等边△ABC中，D是BC的中点，
∴球心O是△ABC的中心，
∴球O的半径为R=OD=$\frac{1}{3}$AD=$\frac{1}{3}$h．
点评 本题考查了空间几何体的位置关系的计算问题，是基础题目．
练习册系列答案
相关题目
14．已知函数f（x$\left\{\begin{array}{l}{|x+2|+a，x≤0}\\{lgx，x＞0}\end{array}\right.$有三个不同零点，则实数a的取值范围为（ ）
| A． | [-2，0） | B． | [-2，+∞） | C． | （-2，0） | D． | （-∞，2] |
16．某电信公司规定，互联网拨号上网用户资源如表：
注：①基本费为每户每月固定缴纳的网络使用费，基本费包含一定量的网络使用时间，用户每月网络使用费不超过基本费的，只收基本费，每月网络使用费超过基本费的，同时加收超过基本费的部分；②月上网费=月基本费+月网络使用费+月通信费．
（1）若某用户以“963”方式上网，上网多长时间，网络使用费达到100元；
（2）分别写出以“963”方式和“169”方式上网的月上网费y（元）与月上网时间t（h）之间的函数关系式；
（3）若某用户平均每月上网时间为120h，试问他用哪种方式上网合算．
| 项目方式 | 基本费 | 网络使用费 | 通信费 |
| 963 | 0 | 0.05元/min | 0.02元/min |
| 169 | 100元/月 | 1元/h |
（1）若某用户以“963”方式上网，上网多长时间，网络使用费达到100元；
（2）分别写出以“963”方式和“169”方式上网的月上网费y（元）与月上网时间t（h）之间的函数关系式；
（3）若某用户平均每月上网时间为120h，试问他用哪种方式上网合算．
好学的小红在学完三角形的角平分线后，遇到下列4个问题，请你帮她解决，如图，在ABC中，∠BAC=50°，点I是两角B、C平分线的交点．
17．已知点M（3，2），点P在y轴上运动，点Q在圆C：（x-1）2+（y+2）2=4上运动，则|$\overrightarrow{MP}+\overrightarrow{MQ}$|的最小值为（ ）
| A． | 3 | B． | 5 | C． | 2$\sqrt{5}$-1 | D． | 2$\sqrt{5}$+1 |