题目内容
14．已知棱长为1的正方体AC1，E、F分别为B1C1和C1D1的中点．（1）求证：E、F、B、D共面；
（2）求证：BE、DF、CC1三线共点；
（3）求棱台C1EF-CBD的体积．
分析 （1）先证BD∥EF，通过EF，BD两直线共面，得E、F、D、B共面；
（2）设BE∩DF=O，证明O∈CC1，即可证明BE、DF、CC1三线共点；
（3）利用两个锥体体积的差求棱台C1EF-CBD的体积．
解答 
（1）证明：∵EF∥D1B1，BD∥D1B1，∴BD∥EF，
∴EF，BD两直线共面，
∴E、F、D、B共面；
（2）证明：设BE∩DF=O，
则O∈平面DC1，O∈平面BC1，
∵平面DC1∩平面BC1=CC1，
∴O∈CC1，
∴BE、DF、CC1三线共点；
（3）解：棱台C1EF-CBD的体积=$\frac{1}{3}×\frac{1}{2}×1×1×2-\frac{1}{3}×\frac{1}{2}×\frac{1}{2}×\frac{1}{2}×1$=$\frac{5}{8}$．
点评 本题考查求棱台C1EF-CBD的体积，考查平面基本性质的运用，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
相关题目
如图，在四棱锥F-ABCD中，侧面ABF⊥底面ABCD，四边形ABCD为矩形，且AB=2，AD=AF=1，∠BAF=60°．O、P分别为AB、CB的中点，M为△OBF的重心．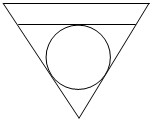
如图，有一横截面为正三角形的圆锥形容器，内部盛水的高度为h，放入一个球后，水面恰好与球相切，求球的半径．