题目内容
15.若f(x)=x3+x2+bx+c有极值点x1,x2且f(x1)=x1,则关于x的方程3(f(x))2+2f(x)+b=0的不同实根个数是3.分析 求导数f′(x),由题意知x1,x2是方程3x2+2x+b=0的两根,从而关于f(x)的方程3(f(x))2+2f(x)+b=0有两个根,作出草图,由图象可得答案.
解答  解:∵f(x)=x3+x2+bx+c有极值点x1,x2,
解:∵f(x)=x3+x2+bx+c有极值点x1,x2,
∴f′(x)=3x2+2x+b,
且x1,x2是方程3x2+2x+b=0的两根,
不妨设x2>x1,
由3(f(x))2+2f(x)+b=0,
则有两个f(x)使等式成立,
x1=f(x1),x2>x1=f(x1),
如图所示:有3个交点,
故答案为:3.
点评 本题主要考查函数零点的概念、函数的极值和函数的导数之间的关系,利用是数形结合是解决本题的关键.

练习册系列答案
相关题目
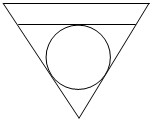 如图,有一横截面为正三角形的圆锥形容器,内部盛水的高度为h,放入一个球后,水面恰好与球相切,求球的半径.
如图,有一横截面为正三角形的圆锥形容器,内部盛水的高度为h,放入一个球后,水面恰好与球相切,求球的半径.