题目内容
15．设某几何体的三视图如图，则该几何体的体积为4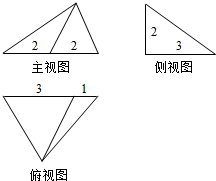
分析 由已知中的三视图，可知该几何体是一个以俯视图为底面的三棱锥，分别求出底面面积和高，代入锥体体积公式，可得答案．
解答 解：由已知中的三视图，可知该几何体是一个以俯视图为底面的三棱锥，
棱锥的底面面积S=$\frac{1}{2}（3+1）×3$=6，
棱锥的高h=2，
故棱锥的体积V=$\frac{1}{3}Sh$=4，
故答案为：4．
点评 本题考查的知识点是由三视图求体积和表面积，解决本题的关键是得到该几何体的形状．
练习册系列答案
津桥教育计算小状元系列答案
相关题目
3．设x0是函数f（x）=2x-|log2x|-1的一个零点，若a＞x0，则f（a）满足（ ）
| A． | f（a）＞0 | B． | f（a）＜0 | ||
| C． | f（a）可以等于0 | D． | f（a）的符号不能确定 |
10．下列集合中，结果是空集的是（ ）
| A． | {x∈R|x2-1=0} | B． | {x|x＞6或x＜1} | C． | {（x，y）|x2+y2=0} | D． | {x|x＞6且x＜1} |
20．i为虚数单位，复平面内表示复数z=$\frac{1}{3+i}$的点在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
4．已知复数z=3-2i-$\frac{5i}{2-i}$，则复数z对应复平面上的点Z位于（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
5．某超市从2014年甲、乙两种酸奶的日销售量（单位：箱）的数据中分別随机抽取100个．整理得到数据分组及频率分布表和频率分布直方图：
（Ⅰ）写出频率分布直方图1中的a的值；并作出甲种酸奶日销售量的频率分布直方图；
（Ⅱ）记甲种酸奶与乙种酸奶日销售量（单位：箱）的方差分别为s${\;}_{1}^{2}$，s${\;}_{2}^{2}$，试比较s${\;}_{1}^{2}$与s${\;}_{2}^{2}$的大小；（只需写出结论）
（Ⅲ）假设同一组中的每个数据可用该该组区间的中点值代替，试估计乙种酸奶在未来一个月（按30天计箅）的销售量总量．
| 分组（日销售量） | 频率（甲种酸奶） |
| [0，10] | 0.10 |
| （10，20] | 0.20 |
| （20，30] | 0.30 |
| （30，40] | 0.25 |
| （40，50] | 0.15 |
（Ⅰ）写出频率分布直方图1中的a的值；并作出甲种酸奶日销售量的频率分布直方图；
（Ⅱ）记甲种酸奶与乙种酸奶日销售量（单位：箱）的方差分别为s${\;}_{1}^{2}$，s${\;}_{2}^{2}$，试比较s${\;}_{1}^{2}$与s${\;}_{2}^{2}$的大小；（只需写出结论）
（Ⅲ）假设同一组中的每个数据可用该该组区间的中点值代替，试估计乙种酸奶在未来一个月（按30天计箅）的销售量总量．