题目内容
9.已知双曲线C与椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1有相同的焦点F1、F2,点P为双曲线C与椭圆的一个交点,且满足|PF1|=2|PF2|,则双曲线C的渐近线方程是( )| A. | y=±$\sqrt{3}$x | B. | y=±$\sqrt{2}$x | C. | y=±x | D. | y=±$\frac{\sqrt{3}}{2}$x |
分析 通过椭圆、双曲线的定义直接计算即可.
解答 解:由椭圆定义可知:|PF1|+|PF2|=6,
又∵|PF1|=2|PF2|,∴3|PF2|=6,即|PF2|=2,
由双曲线定义可知:|PF1|-|PF2|=2a,
又∵|PF1|=2|PF2|,∴|PF2|=2a,即a=1,
由已知,双曲线的焦半距c=2,则b=$\sqrt{3}$,
∴双曲线的渐近线方程为:y=±$\sqrt{3}$x,
故选:A.
点评 本题考查求椭圆的离心率,注意解题方法的积累,属于基础题.

练习册系列答案
相关题目
20.i为虚数单位,复平面内表示复数z=$\frac{1}{3+i}$的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
4.已知复数z=3-2i-$\frac{5i}{2-i}$,则复数z对应复平面上的点Z位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
1.定义在R上的函数f(x)满足:f(x+1)=-f(x),当x∈(0,1]时,f(x)=x+1,则f(3.5)的值是( )
| A. | 0.5 | B. | -1.5 | C. | 2.5 | D. | -2.5 |
18.下列函数中既是奇函数又在区间(0,+∞)上递增的是( )
| A. | y=-3x | B. | y=2x-2-x | C. | y=x2+1 | D. | y=|x| |
19.设a、b、c分别是△ABC的三边长,且a=4,b=5,c=7,则△ABC是( )
| A. | 直角三角形 | B. | 锐角三角形 | C. | 钝角三角形 | D. | 无法确定 |
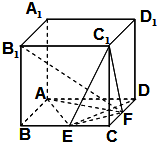 如图,在棱长为2的正方体ABCD-A1B1C1D1中,点E,F分别是棱BC,CD的中点,
如图,在棱长为2的正方体ABCD-A1B1C1D1中,点E,F分别是棱BC,CD的中点,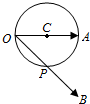 如图,OA为圆C的直径,有向线段OB与圆C交点P,且$\overrightarrow{OP}$=$\frac{1}{2}\overrightarrow{OB}$.若|$\overrightarrow{OB}$|=$\sqrt{3}$,则$\overrightarrow{OA}$•$\overrightarrow{OB}$=$\frac{3}{2}$.
如图,OA为圆C的直径,有向线段OB与圆C交点P,且$\overrightarrow{OP}$=$\frac{1}{2}\overrightarrow{OB}$.若|$\overrightarrow{OB}$|=$\sqrt{3}$,则$\overrightarrow{OA}$•$\overrightarrow{OB}$=$\frac{3}{2}$.