题目内容
8.若向量$\overrightarrow{a}$=(x,3)(x∈R),则“x=4是|$\overrightarrow{a}$|=5”的( )| A. | 充要条件 | B. | 必要不充分条件 | ||
| C. | 充分不必要条件 | D. | 既不充分也不必要条件 |
分析 根据充分条件和必要条件的定义结合向量模长的计算公式进行判断即可.
解答 解:若x=4,则$\overrightarrow{a}$=(4,3),则|$\overrightarrow{a}$|=$\sqrt{{3}^{2}+{4}^{2}}$=5,成立.
若|$\overrightarrow{a}$|=5,则|$\overrightarrow{a}$|=$\sqrt{x^2+3}$=5,即x2=16,解得x=±4,
即“x=4是|$\overrightarrow{a}$|=5”的充分不必要条件,
故选:C
点评 本题主要考查充分条件和必要条件的判断,根据向量的坐标公式是解决本题的关键.

练习册系列答案
相关题目
18.为了考查培育的某种植物的生长情况,从试验田中随机抽取50株该植物进行检测,得到该植物高度的频数分布表如下:
(Ⅰ)写出表中①②③④处的数据;
(Ⅱ)用分层抽样法从第3、4、5组中抽取一个容量为6的样本,则各组应分别抽取多少个个体?
(Ⅲ)在(Ⅱ)的前提下,从抽出的容量为6的样本中随机选取两个个体进行进一步分析,求这两个个体中至少有一个来自第4组的概率.
| 组序 | 高度区间 | 频数 | 频率 |
| 1 | [230,235) | 8 | 0.16 |
| 2 | [235,240) | ① | 0.24 |
| 3 | [240,245) | ② | 0.20 |
| 4 | [245,250) | 10 | ③ |
| 5 | [250,255] | 5 | ④ |
| 合计 | 50 | 1.00 | |
(Ⅱ)用分层抽样法从第3、4、5组中抽取一个容量为6的样本,则各组应分别抽取多少个个体?
(Ⅲ)在(Ⅱ)的前提下,从抽出的容量为6的样本中随机选取两个个体进行进一步分析,求这两个个体中至少有一个来自第4组的概率.
3.设x0是函数f(x)=2x-|log2x|-1的一个零点,若a>x0,则f(a)满足( )
| A. | f(a)>0 | B. | f(a)<0 | ||
| C. | f(a)可以等于0 | D. | f(a)的符号不能确定 |
20.i为虚数单位,复平面内表示复数z=$\frac{1}{3+i}$的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
18.下列函数中既是奇函数又在区间(0,+∞)上递增的是( )
| A. | y=-3x | B. | y=2x-2-x | C. | y=x2+1 | D. | y=|x| |
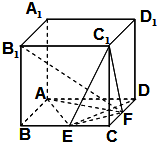 如图,在棱长为2的正方体ABCD-A1B1C1D1中,点E,F分别是棱BC,CD的中点,
如图,在棱长为2的正方体ABCD-A1B1C1D1中,点E,F分别是棱BC,CD的中点,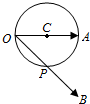 如图,OA为圆C的直径,有向线段OB与圆C交点P,且$\overrightarrow{OP}$=$\frac{1}{2}\overrightarrow{OB}$.若|$\overrightarrow{OB}$|=$\sqrt{3}$,则$\overrightarrow{OA}$•$\overrightarrow{OB}$=$\frac{3}{2}$.
如图,OA为圆C的直径,有向线段OB与圆C交点P,且$\overrightarrow{OP}$=$\frac{1}{2}\overrightarrow{OB}$.若|$\overrightarrow{OB}$|=$\sqrt{3}$,则$\overrightarrow{OA}$•$\overrightarrow{OB}$=$\frac{3}{2}$.