题目内容
16.已知函数$f(x)=\sqrt{3}sin(ωx+φ)(ω>0,-\frac{π}{2}≤φ<\frac{π}{2})$的图象关于直线$x=\frac{π}{3}$对称,且图象上相邻两个最高点的距离为π.(1)求ω和φ的值;
(2)当$x∈[0,\frac{π}{2}]$时,求函数y=f(x)的最大值和最小值.
分析 (1)由题意易得周期为π,可得ω,再由对称轴可得φ值;
(2)利用(1)可得解析式,由x范围结合三角函数的性质可得最值.
解答 解:(1)∵函数f(x)图象上相邻两个最高点的距离为π,
∴?(x)的最小正周期T=π,∴ω=$\frac{2π}{T}$=2,
又∵f(x)图象关于直线x=$\frac{π}{3}$对称,
∴2×$\frac{π}{3}$+φ=kπ+$\frac{π}{2}$,k∈Z,
∵-$\frac{π}{2}$≤φ<$\frac{π}{2}$,∴φ=-$\frac{π}{6}$.
(2)由(1)知f(x)=2sin(2x-$\frac{π}{6}$),
∵x∈[0,$\frac{π}{2}$],
∴2x-$\frac{π}{6}$∈[-$\frac{π}{6}$,$\frac{5π}{6}$],
∴sin(2x-$\frac{π}{6}$)∈[-$\frac{1}{2}$,1],
∴f(x)min=f(0)=-$\frac{\sqrt{3}}{2}$,f(x)max=f($\frac{π}{3}$)=$\sqrt{3}$.
点评 本题考查三角函数的图象和性质,涉及三角函数的对称性和最值,属中档题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
4.下列函数在区间(-∞,0)上为增函数的是( )
| A. | y=x2 | B. | y=$\frac{-2}{x}$ | C. | y=($\frac{1}{2}$)x | D. | y=3-x |
1.下列关系式正确的是( )
| A. | 0∉Z | B. | ∅⊆{0} | C. | ∅∈{0} | D. | 0∈∅ |
8.已知M={x|x2+x-2>0},$N=\{x|\frac{2}{2-x}>1\}$,则M∩N=( )
| A. | {x|1<x<2} | B. | {x|0<x<1} | C. | {x|x<-2或x>1} | D. | {x|-2<x<2} |
5.下列说法中正确的是( )
| A. | 若命题p:x∈R,x2-x-1<0,则¬p:x∈R,x2-x-1>0. | |
| B. | 命题:“若x2=1,则x=1或x=-1”的逆否命题是:“若x≠1且x≠-1,则x2≠1” | |
| C. | “$φ=\frac{π}{2}$”是“y=sin(2x+φ)为偶函数”的充要条件 | |
| D. | 命题p:若$\overrightarrow{a}$=(2,1),$\overrightarrow{b}$=(-1,k2-2),则k=2是$\overrightarrow{a}⊥\overrightarrow{b}$的充分不必要条件;命题q:若幂函数f(x)=xa(a∈R)的图象过点(2,$\frac{\sqrt{2}}{2}$),则f(4)=$\frac{1}{2}$,则p∨(¬q)是假命题 |
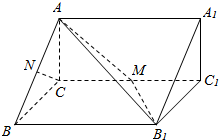 如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,CC1=4,M是棱CC1的中点.
如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,CC1=4,M是棱CC1的中点.