题目内容
设{an}是正数组成的数列,其前n项和为Sn,并且对于所有的n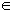 N+,都有
N+,都有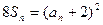 。
。
(1)写出数列{an}的前3项;
(2)求数列{an}的通项公式(写出推证过程);
(3)设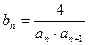 ,
, 是数列{bn}的前n项和,求使得
是数列{bn}的前n项和,求使得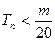 对所有n
对所有n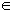 N+都成立的最小正整数
N+都成立的最小正整数 的值。
的值。
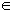 N+,都有
N+,都有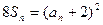 。
。(1)写出数列{an}的前3项;
(2)求数列{an}的通项公式(写出推证过程);
(3)设
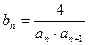 ,
, 是数列{bn}的前n项和,求使得
是数列{bn}的前n项和,求使得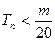 对所有n
对所有n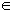 N+都成立的最小正整数
N+都成立的最小正整数 的值。
的值。⑴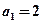 ,
,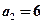 ,
,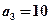 ⑵
⑵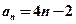 ⑶m的最小值是10
⑶m的最小值是10
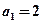 ,
,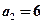 ,
,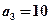 ⑵
⑵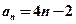 ⑶m的最小值是10
⑶m的最小值是10(1) n=1时  ∴
∴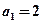
n=2时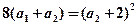 ∴
∴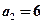
n=3时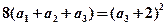 ∴
∴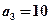
(2)∵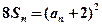 ∴
∴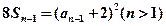
两式相减得: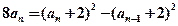 即
即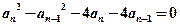
也即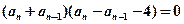
∵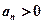 ∴
∴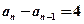 即
即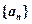 是首项为2,公差为4的等差数列
是首项为2,公差为4的等差数列
∴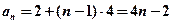
(3)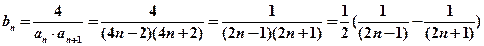
∴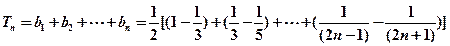

∵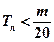 对所有
对所有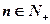 都成立 ∴
都成立 ∴ 即
即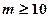
故m的最小值是10 。
 ∴
∴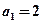
n=2时
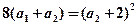 ∴
∴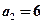
n=3时
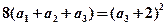 ∴
∴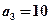
(2)∵
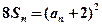 ∴
∴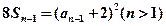
两式相减得:
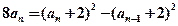 即
即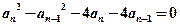
也即
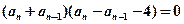
∵
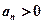 ∴
∴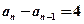 即
即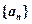 是首项为2,公差为4的等差数列
是首项为2,公差为4的等差数列∴
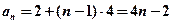
(3)
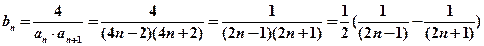
∴
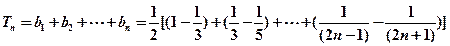

∵
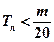 对所有
对所有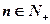 都成立 ∴
都成立 ∴ 即
即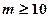
故m的最小值是10 。

练习册系列答案
相关题目
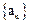 的前n项和为
的前n项和为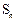 ,对一切正整数n,点
,对一切正整数n,点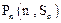 都在函数
都在函数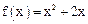 的图像上,且过点
的图像上,且过点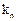 。
。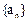 的通项公式;
的通项公式;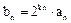 ,求数列
,求数列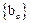 的前n项和
的前n项和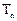 ;
;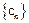 满足
满足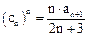 ,求数列
,求数列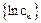 的最值。
的最值。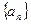 的前n项和为
的前n项和为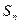 ,且对一切正整数n都有
,且对一切正整数n都有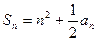 。
。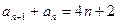 ;(2)求数列
;(2)求数列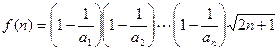 ,
,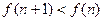 对一切
对一切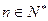 都成立。
都成立。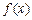 的反函数为
的反函数为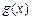 ,且
,且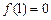 ,若点
,若点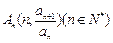 在曲线
在曲线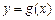 上,
上,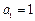 ,对于大于或等于2的任意自然数
,对于大于或等于2的任意自然数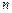 均有
均有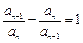 .(Ⅰ)求
.(Ⅰ)求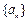 的通项公式;(Ⅲ)设
的通项公式;(Ⅲ)设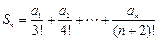 ,求
,求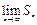 .
. 中,
中,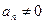 ,且
,且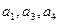 成等比数列,则其公比
成等比数列,则其公比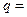 .
.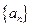 是等差数列,且
是等差数列,且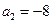 ,
,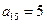 ,
,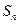 是数列
是数列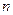 项和,则
项和,则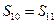
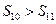
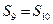
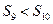
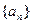 的前n项和为Sn,已知S1,2S2,3S3成等差数列,则
的前n项和为Sn,已知S1,2S2,3S3成等差数列,则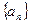 中,
中,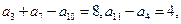 则
则