题目内容
10.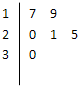 某车间共有12名工人,随机抽取6名作为样本,他们某日加工零件的个数的茎叶图如图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.
某车间共有12名工人,随机抽取6名作为样本,他们某日加工零件的个数的茎叶图如图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.(1)根据茎叶图计算样本均值;
(2)根据茎叶图推断该车间12名工人中有几名优秀工人;
(3)要从这6人中,随机选出2人参加一项技术比武,选出的2人至少有1人为优秀工人的概率.
分析 (1)代入平均数公式即可分别求解;
(2)分别记此六人为A,B,C,D,E,F,求出从中任抽取2人的所有选法的结果,然后求出
高于22的结果数,代入古典概型的概率公式可求
解答 解:(1)由题意可得,样本平均值$\overline{x}=\frac{17+19+20+21+25+30}{6}$=22;
(2)样本中的优秀员工有2人,
所以12名工人中优秀员工有$12×\frac{2}{6}$=4人
(3)分别记此六人为A,B,C,D,E,F,从中任抽取2名学生成绩的所有选法有:(A,B),(A,C),(A,D),(A,E),(A,F),(B,C),(B,D),(B,E),(B,F ),(C,D),(C,E),(C,F),(D,E),(D,F),(E,F)共有15种,
而至少有1人为优秀工人的情况有(A,E),(A,F),(B,E),(B,F ),(C,E),(C,F),(D,E),(D,F),(E,F)共有9种,
所求的概率P=$\frac{9}{15}$=$\frac{3}{5}$.
点评 本题主要考查了茎叶图、一组数据的平均数,及古典概率模型的公式的应用,属于基础试题

练习册系列答案
相关题目
19.如图是一个几何体的三视图,则该几何体任意两个顶点间距离的最大值是( )


| A. | 3$\sqrt{2}$ | B. | 3$\sqrt{3}$ | C. | 4 | D. | 5 |
2.设函数f1(x)=x2,f2(x)=2(x-x2),ai=$\frac{i}{99}$,i=0,1,2,…,99,记Sk=|fk(a1)-fk(a0)|+|fk(a2)-fk(a1)|+…+|fk(a99)-fk(a98)|,k=1,2,则下列结论正确的是( )
| A. | S1=1<S2 | B. | S1=1>S2 | C. | S1>1>S2 | D. | S1<1<S2 |
19.直线l1:ρsin(θ+α)=a和l2:θ=$\frac{π}{2}$-α的位置关系是( )
| A. | l1∥l2 | B. | l1⊥l2 | C. | l1和l2重合 | D. | l1,l2斜交 |
 如图AB是圆O的一条弦,过点A作圆的切线AD,作BC⊥AC,与该圆交于点D,若AC=2$\sqrt{3}$,CD=2.
如图AB是圆O的一条弦,过点A作圆的切线AD,作BC⊥AC,与该圆交于点D,若AC=2$\sqrt{3}$,CD=2.