题目内容
7.已知k是整数,∠A、∠B、∠C为钝角△ABC的三个内角,且其对边分别为a、b、c.(1)若方程x2-2kx+3k2-7k+3=0有实根,求k的值;
(2)对于(1)中的k的值,若sinC=$\frac{k}{\sqrt{2}}$,且有关系式(c-b)sin2A+bsin2B=csin2C,试求∠A、∠B、∠C的度数.
分析 (1)由二次方程有实根的条件得:△=4k2-4(3k2-7k+3)≥0,化简求出不等式的解,根据k是整数得到k的值;
(2)由(1)和正弦函数的范围求出sinC,由内角的范围求出∠C,根据正弦定理化简已知的式子,结合条件和余弦定理求出∠A,再求出∠B、∠C的度数.
解答 解:(1)∵方程x2-2kx+3k2-7k+3=0有实根,
∴△=4k2-4(3k2-7k+3)≥0,则2k2-7k+3≤0,
解得$\frac{1}{2}≤k≤3$,
∵k是整数,∴k的值是1、2、3;
(3)∵sinC=$\frac{k}{\sqrt{2}}$≤1,∴由(1)知k=1符合,则sinC=$\frac{\sqrt{2}}{2}$,
∴∠C=45°或135°,
∵(c-b)sin2A+bsin2B=csin2C,
∴由正弦定理得,(c-b)a2+b3=c3,
化简得,(c-b)a2=(c-b)(b2+bc+c2),
∵△ABC是钝角三角形,且∠C=45°或135°,
∴c-b≠0,则a2=b2+bc+c2,即b2+c2-a2=-bc,
由余弦定理得,cosA=$\frac{{b}^{2}+{c}^{2}{-a}^{2}}{2bc}$=$-\frac{1}{2}$,
∴∠A=120°,∠C=45°,则∠B=180°-A-C=180°-120°-45°=15°,
即∠A、∠B、∠C的度数分别是120°、45°、15°.
点评 本题考查了正弦、余弦定理,内角和定理,正弦三角函数的值域,以及二次方程、不等式等,考查的知识点较多,属于中档题.

练习册系列答案
相关题目
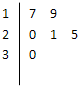 某车间共有12名工人,随机抽取6名作为样本,他们某日加工零件的个数的茎叶图如图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.
某车间共有12名工人,随机抽取6名作为样本,他们某日加工零件的个数的茎叶图如图所示,其中茎为十位数,叶为个位数,日加工零件个数大于样本均值的工人为优秀工人.